PlaidCTF 2023 Writeups

Changelog (last updated 2023-04-19)

Update 2023-04-19: Added more efficient intended and easier unintended solutions to Disk A

Update 2023-04-18: Added full solution scripts

bivalves
fastrology
The Other CSS
- Disk A
- Disk B

bivalves

By mserrano and ubuntor

Yarr! Me lunch is clams and me dinner is mussels. Be there a pearl inside?

Attachment: bivalves.tgz

39 solves, 78 points

Challenge bivalves.pypython
from bitstream import BitStream
from bitstring import BitArray
import os

KEY = BitArray(os.urandom(10)).bin
IV = BitArray(os.urandom(10)).bin

print(IV)

state = BitArray(bin=(KEY + '0101000001010' + IV + '0'*4))
output_stream = BitStream()

def step(out=True):
    if out:
        output_stream.write(state[65] ^ state[92], bool)
    t1 = state[65] ^ state[92] ^ (state[90] & state[91]) ^ state[170]
    t2 = state[161] ^ state[176] ^ (state[174] & state[175]) ^ state[68]
    for i in range(92, 0, -1):
        state.set(state[i - 1], i)
    state.set(t2, 0)
    for i in range(176, 93, -1):
        state.set(state[i - 1], i)
    state.set(t1, 93)

for _ in range(708):
    step(False)

pt=BitArray(bytes=('''There once was a ship that put to sea
The name of the ship was the Billy O' Tea
The winds blew up, her bow dipped down
Oh blow, my bully boys, blow (huh)

Soon may the Wellerman come
To bring us sugar and tea and rum
One day, when the tonguing is done
We'll take our leave and go

She'd not been two weeks from shore
When down on her right a whale bore
The captain called all hands and swore
He'd take that whale in tow (huh)

Soon may the Wellerman come
To bring us sugar and tea and rum
One day, when the tonguing is done
We'll take our leave and go

- '''.encode('utf-8') + (open('flag.txt', 'rb').read())))

ciphertext = BitStream()
for i in range(len(pt)):
    step()
    ciphertext.write(output_stream.read(bool, 1)[0] ^ pt[i], bool)

print(ciphertext.read(bytes, len(pt) // 8))

Challenge handout.txt
text
01011010000111001011101010000011001000001111001110010111010001011000101011111111
b'\n_\x02s\xe6\xb4\xf5\xec\xfe\xd6\xb0\xb6\xfb\xf1\x9ab\xb7\x85p(p\x8e\xaf/\xa4[...more...]-?\xca'

A LFSR-like system is used to encrypt a known text. We can ignore the key and IV completely and recover the xorpad by xor-ing plaintext with the handout ciphertext, then use z3 to recover the cipher state at the end of the plaintext section to extend the xorpad and recover the flag.

Solve scriptpython
from bitstring import BitArray
from z3 import *

# Recover parameters

f = open("handout/handout.txt")
f.readline()
ct = eval(f.readline())

ct = BitArray(bytes=ct)

pt=BitArray(bytes=('''There once was a ship that put to sea
The name of the ship was the Billy O' Tea
The winds blew up, her bow dipped down
Oh blow, my bully boys, blow (huh)

Soon may the Wellerman come
To bring us sugar and tea and rum
One day, when the tonguing is done
We'll take our leave and go

She'd not been two weeks from shore
When down on her right a whale bore
The captain called all hands and swore
He'd take that whale in tow (huh)

Soon may the Wellerman come
To bring us sugar and tea and rum
One day, when the tonguing is done
We'll take our leave and go

- '''.encode('utf-8')))

xorpad = ct[:len(pt)] ^ pt

# Model LFSR-like system

initial_state = [BitVec(f"is_{i}", 1) for i in range(177)]

s = Solver()
state = list(initial_state)
counter = 0
outstream = []
def step():
    global outstream, counter
    outstream.append(state[65] ^ state[92])
    t1r = state[65] ^ state[92] ^ (state[90] & state[91]) ^ state[170]
    t2r = state[161] ^ state[176] ^ (state[174] & state[175]) ^ state[68]

    t1 = BitVec(f"t1_{counter}", 1)
    t2 = BitVec(f"t2_{counter}", 1)
    s.add(t1 == t1r)
    s.add(t2 == t2r)

    for i in range(92, 0, -1):
        state[i] = state[i - 1]
    state[0] = t2
    for i in range(176, 93, -1):
        state[i] = state[i - 1]
    state[93] = t1
    counter += 1

for i in range(len(pt)):
    step()
    s.add(outstream[i] == xorpad.bin[i])

ends = []
for i in range(len(ct) - len(pt)):
    step()
    end = BitVec(f"e_{counter}", 1)
    s.add(outstream[len(pt) + i] == end)
    ends.append(end)

print(s.check())

# Recover flag

m = s.model()
res = BitArray(bin="".join([
    str(m[i].as_long())
    for i in ends
])) ^ ct[len(pt):]
print(res.bytes.decode())

output

sat
pctf{but_the_whale_is_covered_in_barnacles}

fastrology

By ubuntor and strikeskids

Any ol’ pirate knows how to navigate by the stars, but only a great one knows how to do it fast. Let’s see which one you are.

nc fastrology.chal.pwni.ng 1337

Attachment: fastrology.tar.gz

Challenge server.pypython
import sys
import string
import random
import hashlib
import time
import subprocess

FLAGS = [
    '<real new moon flag is on the server>',
    '<real waxing crescent flag is on the server>',
    '<real waxing gibbous flag is on the server>',
    '<real full moon flag is on the server>'
]
NUM_TRIALS = 50
PHASES = ['new moon', 'waxing crescent', 'waxing gibbous', 'full moon']
PHASE_FILES = ['new_moon.js', 'waxing_crescent.js', 'waxing_gibbous.js', 'full_moon.js']
MAXTIMES = [15, 15, 15, 30]
USE_POW = True

if USE_POW:
    # proof of work
    prefix = ''.join(random.choice(string.ascii_letters + string.digits) for i in range(10))
    print("Give me a string starting with {} of length {} so its sha256sum ends in ffffff.".format(prefix, len(prefix)+8), flush=True)
    l = input().strip()
    if len(l) != len(prefix)+8 or not l.startswith(prefix) or hashlib.sha256(l.encode('ascii')).hexdigest()[-6:] != "ffffff":
        print("Nope.", flush=True)
        sys.exit(1)

while True:
    phase = input(f'which phase? [{", ".join(PHASES)}]\n')
    if phase not in PHASES:
        continue
    phase = PHASES.index(phase)
    break

for trial in range(NUM_TRIALS):
    print(f'{PHASES[phase]}: trial {trial+1}/{NUM_TRIALS}', flush=True)
    tick = time.time()
    p = subprocess.run(['node', PHASE_FILES[phase]])
    tock = time.time()
    if abs(tock-tick) > MAXTIMES[phase]:
        print(f'⌛️❗️ ({tock-tick:.3f})', flush=True)
        sys.exit(1)
    if p.returncode != 42:
        print(f'🔮️🚫️❗️', flush=True)
        sys.exit(1)

print('congrats!', flush=True)
print(FLAGS[phase])

There are multiple javascript programs that generate a data string using an alphabet by sampling characters using alphabet[Math.floor(Math.random() * alphabet.length)]. The task is to recover the internal random state using this “prefix” and predict the characters that will be generated after the prefix.

Challenge helper functionspython
import string
import hashlib
import random
from pwn import *

DEBUG = False

def solve_pow(prefix):
    POW_CHARSET = string.ascii_letters + string.digits
    assert len(prefix) == 10

    print(f"solving pow {prefix}")
    ctr = 0
    while True:
        ctr += 1
        if ctr % 0x100000 == 0:
            print(".", end="", flush=True)
        guess = prefix + "".join(random.choices(POW_CHARSET, k=8))
        if hashlib.sha256(guess.encode('ascii')).hexdigest()[-6:] != "ffffff":
            continue
        print(" " + guess)
        return guess

r = None
charset = None
def connect_to_challenge(sub_challenge_name, use_charset):
    global r, charset
    if DEBUG:
        r = process(["python", "localrun.py"]) # local copy of server.py
    else:
        r = remote("fastrology.chal.pwni.ng", 1337)
        r.recvuntil(b"with ")
        pow_chal = r.recvline().decode().strip().split()[0]
        r.sendline(solve_pow(pow_chal).encode())
    r.sendline(sub_challenge_name.encode())
    charset = use_charset

def moon_to_buckets(moon):
    return [ charset.index(i) for i in moon ]
def buckets_to_moon(buckets):
    return "".join([ charset[i] for i in buckets ])

chal_hash = None
def get_challenge():
    global chal_hash
    r.recvuntil(b"trial")
    r.recvline()
    chal_prefix = r.recvline().decode().strip()
    print("challenge:", chal_prefix[:20])
    chal_prefix = moon_to_buckets(chal_prefix)
    chal_hash = r.recvline().decode().strip()
    return chal_prefix

def answer_challenge(ans, do_send=False):
    ans = buckets_to_moon(ans)
    if hashlib.md5(ans.encode()).hexdigest() == chal_hash:
        print("answer:", ans[:20])
        r.sendline(ans.encode())
        return True
    else:
        return False

def claim_flag():
    global r
    r.recvuntil(b"congrats!\n")
    flag = r.recvline().decode()
    r = r.close()
    print(flag)
    return flag

Because the sampling code uses Math.floor(), we can infer the high bits of each call to Math.random(). Existing solutions for breaking this PRNG use z3 to solve for random state, but this generally requires many more high bits of information per call to finish calculating within a reasonable amount of time. Regardless, these implementations can help us understand how to convert PRNG states to 64-bit floats and vice versa.

Type conversion helperspython
import struct

def f64_to_u64(f):
    # f64 in [0, 1) to u64 XorShift128 state
    if f == 1.0:
        return 0xffffffffffffffff
    buf = struct.pack("d", f + 1)
    u52 = struct.unpack("<Q", buf)[0] & 0x000fffffffffffff
    u64 = u52 << 12
    return u64

def u64_to_f64(u):
    # u64 XorShift128 state to f64 in [0, 1)
    buf = struct.pack("<Q", (u >> 12) | 0x3FF0000000000000)
    f64 = struct.unpack("d", buf)[0] - 1
    return f64

static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
    uint64_t s1 = *state0;
    uint64_t s0 = *state1;
    *state0 = s0;
    s1 ^= s1 << 23;
    s1 ^= s1 >> 17;
    s1 ^= s0;
    s1 ^= s0 >> 26;
    // s1 = (s1 << 23) ^ (s1 >> 17) ^ s0 ^ (s0 >> 26)
    *state1 = s1;
  }

Referring to nodejs source, the javascript PRNG has a 128-bit initial state (64-bit s0 and 64-bit s1) future 64-bit states are linear combinations of previous states. We can model the initial PRNG state as 128 numbers in GF(2) and model future states as the sum of 64 subsets of the original 128 numbers.

Implementing symbolic PRNG statepython
class BV:
    def __init__(self, data):
        # data is 64-long list of 128 bit ints
        # data[0] is a 128 bit int indicating the mask of bits in s0s1
        #   which are xor-ed together to generate the 0th (LSB) bit of
        #   this state
        # Low 64 bits of s0s1 come from s0, high 64 bits come from s1
        assert(len(data) == 64)
        self.data = data

    def __xor__(self, other):
        return BV([i ^ j for i, j in zip(self.data, other.data)])

    def __lshift__(self, other):
        # After left shift the least significant bits of the state
        # should be empty
        return BV([0] * other + self.data[:-other])

    def __rshift__(self, other):
        # After right shift the most significant bits of the state
        # should be empty
        return BV(self.data[other:] + [0] * other)

    def coef(self, pos):
        # Converts 128 bit mask into list of ints
        coef = f"{self.data[pos]:0128b}"
        coef = [int(i) for i in coef[::-1]]
        return coef

    def eval_one(self, s0s1, pos):
        # From a known s0s1, evalute the bit at one position
        val = sum([i * j for i, j in zip(self.coef(pos), s0s1)]) % 2
        return val

    def eval_all(self, s0s1):
        # From a known s0s1, evalute the bit at all positions and get
        # the u64 output
        vals = [self.eval_one(s0s1, pos) for pos in range(64)]
        vals = "".join([str(i) for i in vals[::-1]])
        vals = int(vals, 2)
        return vals

def xs128p(state0, state1):
    s1 = state0
    s0 = state1

    s1 = s1 ^ (s1 << 23)
    s1 = s1 ^ (s1 >> 17)
    s1 = s1 ^ s0
    s1 = s1 ^ (s0 >> 26)

    output_state = state0
    state0 = state1
    state1 = s1

    return state0, state1, output_state

# Initial symbolic values of s0 and s1
BV.s0 = BV([1 << i for i in range(64)])
BV.s1 = BV([1 << i for i in range(64, 128)])

python

s0, s1 = BV.s0, BV.s1
s0, s1, output_state_0 = xs128p(s0, s1)
s0, s1, output_state_1 = xs128p(s0, s1)
s0, s1, output_state_2 = xs128p(s0, s1)

symbolic_state_2_bit_30 = f"{output_state_2.data[30]:0128b}"
print("The 30th bit of rng[2] depends on these bits of s0 and s1:")
print(f"s0 mask: {symbolic_state_2_bit_30[64:]}")
print(f"s1 mask: {symbolic_state_2_bit_30[:64]}")

output

The 30th bit of rng[2] depends on these bits of s0 and s1:
s0 mask: 0000000000000000100000000000000001000001000000000000000010000000
s1 mask: 0000000100000000000000000000000001000000000000000000000000000000

Each high bit of Math.random() that we obtain from observing the prefix will correspond to one such subset and thus we can apply constrains on the final values derived from said subset. This is equivalent to a system of equations in GF(2) with 128 unknowns and as many equations as there are known bits from the sampled sequence, which means it is solved efficiently with sagemath.

Another notable property of the javascript PRNG involves the order of which random states are returned. The PRNG generates 64 random states at a time and these are returned last-in-first-out, i.e. rng[63] then rng[62], rng[61], … , rng[0], rng[127], … , rng[64], rng[191] and so on. Each challenge will clock the PRNG anywhere from 0 to 63 times before it is used in generating the sampled characters. This will affect any symbolic execution of the PRNG, so this “offset” needs to be brute forced. We can confirm that we have the correct offset when the final answer to each challenge matches the md5 hash given by the challenge server.

Implementing PRNG schedule and precomputing statespython
def schedule_sequence(seq):
    assert(len(seq) % 64 == 0) # ensure block aligned
    return [
        j
        for i in range(0, len(seq), 64)
        for j in seq[i:i+64][::-1]
    ]

n_steps = 64 * 70
s0, s1 = BV.s0, BV.s1
prng_states = []
for _ in range(n_steps):
    s0, s1, output_state = xs128p(s0, s1)
    prng_states.append(output_state)
prng_states = schedule_sequence(prng_states)

The following sections detail the specific solutions for each sub-challenge. A full solve script for all sub-challenges can be found here.

waxing crescent

30 solves, 100 points

Challenge waxing_crescent.jsjs
const { randomInt, createHash } = require("node:crypto");
const readline = require("node:readline").createInterface({
  input: process.stdin,
  output: process.stdout,
});

const warmup_len = randomInt(64);
for (let i = 0; i < warmup_len; i++) {
  Math.random();
}

const prefix_len = 135;
const alphabet = "☊☋☌☍";

let output = "";
for (let i = 0; i < prefix_len + 128; i++) {
  output += alphabet[Math.floor(Math.random() * alphabet.length)];
}

const prefix = output.substring(0, prefix_len);
const expected = output.substring(prefix_len);

console.log(prefix);
console.log(createHash("md5").update(expected, "utf8").digest("hex"));

readline.question("❓️\n", (guess) => {
  readline.close();
  if (guess === expected) {
    console.log("✅");
    process.exit(42);
  } else {
    console.log("❌");
    process.exit(1);
  }
});

There are 4 characters in the alphabet. Each character corresponds to floats in the range of $\left[0, 0.25\right)$ , $\left[0.25, 0.5\right)$ and so on. Notably, the integer representation of all floats in the first bucket will have high bits 00, the second will have high bits 01 and so on. This works because the range of 64-bit integers will be split evenly across 4 buckets which is a power of 2.

python

print(f"{f64_to_u64(0.0)  = :064b}")
print(f"{f64_to_u64(0.1)  = :064b}")
print(f"{f64_to_u64(0.2)  = :064b}")
print(f"{f64_to_u64(0.25) = :064b}")

output

f64_to_u64(0.0)  = 0000000000000000000000000000000000000000000000000000000000000000
f64_to_u64(0.1)  = 0001100110011001100110011001100110011001100110011010000000000000
f64_to_u64(0.2)  = 0011001100110011001100110011001100110011001100110011000000000000
f64_to_u64(0.25) = 0100000000000000000000000000000000000000000000000000000000000000

For each letter in the prefix we can recover these high 2 bits of each PRNG output. This data can be combined with the scheduled prng_states to generate a system of equations; across 135 samples we have 270 constraints and can and solve for the original prng_state. Future Math.random() can be calculated to predict the secret characters and obtain the flag.

python

moon_to_fixed_msb = {
    0: '00', 1: '01', 2: '10', 3: '11'
}

waxing crescent solverpython
from sage.all_cmdline import Matrix, vector, GF

moon_to_fixed_msb_precomp = {
    k: [(63 - idx, int(fix_bit)) for idx, fix_bit in enumerate(v)]
    for k, v in moon_to_fixed_msb.items()
}

F = GF(2)

connect_to_challenge("waxing crescent", "☊☋☌☍")

for trial in range(50):
    print(f"trial {trial}")
    moons = get_challenge()

    for offset in range(64):
        system_mat = []
        system_vec = []
        math_random = iter(prng_states)

        for _ in range(offset):
            next(math_random)
        for moon in moons:
            moon_prng_state = next(math_random)
            for bit_pos, fix_value in moon_to_fixed_msb_precomp[moon]:
                system_mat.append(moon_prng_state.coef(bit_pos))
                system_vec.append(fix_value)

        try:
            s0s1 = Matrix(F, system_mat).solve_right(vector(F, system_vec))
            print(f"Found s0s1 with {offset = }")
        except ValueError:
            # no solution, offset is wrong
            continue

        soln = [
            int(u64_to_f64(prng_state.eval_all(s0s1)) * 4)
            for prng_state in prng_states[offset + 135: offset + 135 + 128]
        ]

        if answer_challenge(soln):
            break

    raise ValueError("No solution found")

flag = claim_flag()

output

..... SwB6JSDCUx5Yb2RLMX
trial 0
challenge: ☋☊☌☌☍☌☊☊☊☌☍☌☍☌☋☋☋☌☊☋
Found s0s1 with offset = 40
Found s0s1 with offset = 41
answer: ☍☌☋☌☌☊☊☍☍☌☋☌☍☋☌☌☋☊☍☍
trial 1
challenge: ☋☊☋☌☋☋☊☍☌☋☊☋☊☍☍☌☋☌☍☌
Found s0s1 with offset = 3
answer: ☌☊☌☍☍☍☌☊☊☍☌☋☋☌☌☊☍☍☌☌
trial 2
[...many lines...]
trial 49
challenge: ☌☊☌☌☍☊☌☌☊☌☌☋☊☊☊☊☊☋☊☋
Found s0s1 with offset = 43
answer: ☍☋☊☊☍☍☍☋☍☊☍☊☊☌☌☍☍☍☊☌
PCTF{moon_wobbles_from_libration_are_kinda_freaky_0bacbc2a52}

new moon

27 solves, 125 points

Challenge new_moon.jsjs
const { randomInt, createHash } = require("node:crypto");
const readline = require("node:readline").createInterface({
  input: process.stdin,
  output: process.stdout,
});

const warmup_len = randomInt(64);
for (let i = 0; i < warmup_len; i++) {
  Math.random();
}

const prefix_len = 192;
const alphabet = "♈♉♊♋♌♍♎♏♐♑♒♓⛎";

let output = "";
for (let i = 0; i < prefix_len + 128; i++) {
  output += alphabet[Math.floor(Math.random() * alphabet.length)];
}

const prefix = output.substring(0, prefix_len);
const expected = output.substring(prefix_len);

console.log(prefix);
console.log(createHash("md5").update(expected, "utf8").digest("hex"));

readline.question("❓️\n", (guess) => {
  readline.close();
  if (guess === expected) {
    console.log("✅");
    process.exit(42);
  } else {
    console.log("❌");
    process.exit(1);
  }
});

There are 13 characters in the alphabet. It is no longer a power of 2 and so it is less clear what each character may imply about the random state. However, by checking the possible high bits of floats in the range of $\left[0, \frac{1}{13}\right)$ , $\left[\frac{1}{13}, \frac{2}{13}\right)$ etc. , we can choose to only constrain the high bits are the same for all floats in that range. Using 192 samples and around 2.15 expected constrained bits per sample, we will obtain around 413 constraints each time which is enough to solve for the PRNG state.

Deriving moon_to_fixed_msbpython
def tand(a, b):
    return "".join([
        i if i == j else "?"
        for i, j in zip(a, b)
    ])

high_bits_max_precision = 12
def fmt(x):
    return f"{x:012b}"

def generate_moon_to_fixed_msb(n_buckets):
    fractions = [
        f64_to_u64(i / n_buckets) >> (64 - high_bits_max_precision)
        for i in range(0, n_buckets+1)
    ]
    moon_to_fixed_msb = {}
    for idx, (i, j) in enumerate(zip(fractions, fractions[1:])):
        acc = fmt(i)
        for k in range(i, j + 1):
            acc = tand(acc, fmt(k))
        moon_to_fixed_msb[idx] = acc.rstrip("?")

    return moon_to_fixed_msb

moon_to_fixed_msb = generate_moon_to_fixed_msb(13)

print(f"{moon_to_fixed_msb = }")

python

moon_to_fixed_msb = {
    0: '000', 1: '00', 2: '001',
    3: '0', 4: '01', 5: '011',
    6: '', 7: '100', 8: '10',
    9: '1', 10: '110', 11: '11',
    12: '111'
}

new moon solverpython
from sage.all_cmdline import Matrix, vector, GF

moon_to_fixed_msb_precomp = {
    k: [(63 - idx, int(fix_bit)) for idx, fix_bit in enumerate(v)]
    for k, v in moon_to_fixed_msb.items()
}

F = GF(2)

connect_to_challenge("new moon", "♈♉♊♋♌♍♎♏♐♑♒♓⛎")

for trial in range(50):
    print(f"trial {trial}")
    moons = get_challenge()
    ok = False

    for offset in range(64):
        system_mat = []
        system_vec = []
        math_random = iter(prng_states)

        for _ in range(offset):
            next(math_random)
        for moon in moons:
            moon_prng_state = next(math_random)
            for bit_pos, fix_value in moon_to_fixed_msb_precomp[moon]:
                system_mat.append(moon_prng_state.coef(bit_pos))
                system_vec.append(fix_value)

        try:
            s0s1 = Matrix(F, system_mat).solve_right(vector(F, system_vec))
            print(f"Found s0s1 with {offset = }")
        except ValueError:
            # no solution, offset is wrong
            continue

        soln = [
            int(u64_to_f64(prng_state.eval_all(s0s1)) * 13)
            for prng_state in prng_states[offset + 192: offset + 192 + 128]
        ]

        if answer_challenge(soln):
            ok = True
            break

    if not ok:
        raise ValueError("No solution found")

flag = claim_flag()

output

solving pow 3Vhp7fapiX
.................................. 3Vhp7fapiXuWoqhzer
trial 0
challenge: ♈♓♐♈♓♉♊♒⛎♑♉♐♉♊♎⛎♊♓♓♍
Found s0s1 with offset = 20
answer: ♐♋♏♉♋♑⛎♒♎♌♓♉♎♊♌♒♍♓♍♍
trial 1
challenge: ♊♉♓♊♍⛎♈♍♌♑♓♌♋♉♌♍⛎♉♏♑
Found s0s1 with offset = 17
answer: ♋♓⛎♒♍♐♏♈♎♓♉⛎♏♑♉♍♊♓♑⛎
trial 2
[...many lines...]
trial 49
challenge: ♎♒♋♋♏⛎♏♑⛎♑♍♉♌♑♐⛎♐♉♒⛎
Found s0s1 with offset = 51
answer: ♋♐♍♍♍♐♈♉♋♓♋♈⛎♈♈♏♋♐♑⛎
PCTF{why_are_there_so_many_named_features_of_the_moon_12d4edbc6c}

full moon

25 solves, 100 points

Challenge full_moon.jsjs
const { randomInt, createHash } = require("node:crypto");
const readline = require("node:readline").createInterface({
  input: process.stdin,
  output: process.stdout,
});

const warmup_len = randomInt(64);
for (let i = 0; i < warmup_len; i++) {
  Math.random();
}

const prefix_len = 600;
const alphabet = "☿♀♁♂♃♄♅♆♇";

let output = "";
for (let i = 0; i < prefix_len + 128; i++) {
  let index = Math.floor(Math.random() * alphabet.length);
  let rand_max = Math.floor(Math.random() * 4);
  let distortion_len = Math.floor(i / 125);
  for (let j = 0; j < distortion_len; j++) {
    index ^= Math.floor(Math.random() * rand_max);
  }
  index = Math.min(index, alphabet.length - 1);
  output += alphabet[index];
}

const prefix = output.substring(0, prefix_len);
const expected = output.substring(prefix_len);

console.log(prefix);
console.log(createHash("md5").update(expected, "utf8").digest("hex"));

readline.question("❓️\n", (guess) => {
  readline.close();
  if (guess === expected) {
    console.log("✅");
    process.exit(42);
  } else {
    console.log("❌");
    process.exit(1);
  }
});

There are now 9 characters in the alphabet but starting from the 125th sample there will be random noise added to the character sampling process. We can generate a similar moon_to_fixed_msb as in new moon for early samples without noise, but for later samples we need to group samples of characters 0-3, 4-7 together and only enforce the bits where they share values. Character 8 will not be affected by noise and we can apply full constraints.

Deriving distorted_moon_to_fixed_msbpython
moon_to_fixed_msb = generate_moon_to_fixed_msb(9)

distorted_moon_to_fixed_msb = dict(moon_to_fixed_msb)

for i in range(0, 8, 4):
    acc = moon_to_fixed_msb[i]
    for j in range(i, i+4):
        acc = tand(acc, moon_to_fixed_msb[j])
    acc = acc.rstrip("?")
    for j in range(i, i+4):
        distorted_moon_to_fixed_msb[j] = acc

print(f"{moon_to_fixed_msb = }")
print(f"{distorted_moon_to_fixed_msb = }")

python

moon_to_fixed_msb = {
    0: '000', 1: '00', 2: '0', 3: '01',
    4: '', 5: '10', 6: '1', 7: '11',
    8: '111'
}
distorted_moon_to_fixed_msb = {
    0: '0', 1: '0', 2: '0', 3: '0',
    4: '', 5: '', 6: '', 7: '',
    8: '111'
}

full moon solverpython
from sage.all_cmdline import Matrix, vector, GF

moon_to_fixed_msb_precomp = {
    k: [(63 - idx, int(fix_bit)) for idx, fix_bit in enumerate(v)]
    for k, v in moon_to_fixed_msb.items()
}

distorted_moon_to_fixed_msb_precomp = {
    k: [(63 - idx, int(fix_bit)) for idx, fix_bit in enumerate(v)]
    for k, v in distorted_moon_to_fixed_msb.items()
}

F = GF(2)

connect_to_challenge("full moon", "☿♀♁♂♃♄♅♆♇")

for trial in range(50):
    print(f"trial {trial}")
    moons = get_challenge()
    ok = False

    for offset in range(64):
        system_mat = []
        system_vec = []
        math_random = iter(prng_states)

        for _ in range(offset):
            next(math_random)
        for moon_idx, moon in enumerate(moons):
            moon_prng_state = next(math_random)
            rand_max = next(math_random)

            use_msbs = moon_to_fixed_msb_precomp[moon]
            if moon_idx >= 125:
                use_msbs = distorted_moon_to_fixed_msb_precomp[moon]

            for bit_pos, fix_value in use_msbs:
                system_mat.append(moon_prng_state.coef(bit_pos))
                system_vec.append(fix_value)
            for distortion_count in range(moon_idx // 125):
                distortion = next(math_random)

        try:
            s0s1 = Matrix(F, system_mat).solve_right(vector(F, system_vec))
            print(f"Found s0s1 with {offset = }")
        except ValueError:
            # no solution, offset is wrong
            continue

        soln = []
        def rng(n):
            return int(u64_to_f64(next(math_random).eval_all(s0s1)) * n)
        for moon_idx in range(600, 600 + 128):
            moon = rng(9)
            rand_max = rng(4)
            for distortion_count in range(moon_idx // 125):
                moon ^= rng(rand_max)
            moon = min(moon, 8)
            soln.append(moon)

        if answer_challenge(soln):
            ok = True
            break

    if not ok:
        raise ValueError("No solution found")

flag = claim_flag()

output

solving pow nQrCJrVCAn
........ nQrCJrVCAn4WT28Q2Z
trial 0
challenge: ☿♂♃♀♇♅♃♁♁♃☿☿♅♄♃♄♃♄♀♆
Found s0s1 with offset = 28
Found s0s1 with offset = 29
answer: ♆♇♁♂☿♀♀♂♆☿♇♆♅☿♀♄♇♃♄☿
trial 1
challenge: ♁♂♂♂♆♅♆♃♃♇♆♂♁♄♃♇♆♂☿♂
Found s0s1 with offset = 39
answer: ♇♀♄♅♃♅♄☿♃♂♃♀♃♅♆♂☿♄♁♆
trial 2
[...many lines...]
trial 49
challenge: ♅♅♇♄♇♂☿☿♇☿♅♀♇♇♂♂♄♆♄♀
Found s0s1 with offset = 23
answer: ♄♃♄♄♃♀☿♅♂♃☿♅♁♂♆♂♇♇♀♆
PCTF{THE_MOON_THE_MOON_THE_MOON_THE_MOON_THE_MOON_50c314a8ac}

waxing gibbous

16 solves, 125 points

Challenge waxing_gibbous.jsjs
const { randomInt, createHash } = require("node:crypto");
const readline = require("node:readline").createInterface({
  input: process.stdin,
  output: process.stdout,
});

const warmup_len = randomInt(64);
for (let i = 0; i < warmup_len; i++) {
  Math.random();
}

const prefix_len = 250;
const alphabet = "♈♉♊♋♌♍♎♏♐♑♒♓⛎";

let backup = "";
for (let i = 0; i < prefix_len + 128; i++) {
  let index = Math.floor(Math.random() * 12);
  backup += alphabet[index];
}

let output = "";
for (let i = 0; i < prefix_len + 128; i++) {
  let index = Math.floor(Math.random() * alphabet.length);
  if (index === 12) {
    // OPHIUCHUS MUST BE CONCEALED
    output += backup[i];
  } else {
    output += alphabet[index];
  }
}

const prefix = output.substring(0, prefix_len);
const expected = output.substring(prefix_len);

console.log(prefix);
console.log(createHash("md5").update(expected, "utf8").digest("hex"));

readline.question("❓️\n", (guess) => {
  readline.close();
  if (guess === expected) {
    console.log("✅");
    process.exit(42);
  } else {
    console.log("❌");
    process.exit(1);
  }
});

There are again 13 characters but any instance of character 12 will be replaced by some other random character. Conversely, all samples we observe may have originally been a 12 but was randomized to something else. Instead, we only apply constraints to bits which would have had the same value regardless if it was changed from 12 or was originally sampled.

Deriving moon_to_fixed_msbpython
moon_to_fixed_msb = generate_moon_to_fixed_msb(13)

ophiuchus_mask = moon_to_fixed_msb[12]
moon_to_fixed_msb = {
    k: tand(ophiuchus_mask, v).rstrip("?")
    for k, v in moon_to_fixed_msb.items()
}

print(f"{moon_to_fixed_msb = }")

python

moon_to_fixed_msb = {
    0: '', 1: '', 2: '??1',
    3: '?', 4: '?1', 5: '?11',
    6: '', 7: '1', 8: '1',
    9: '1',10: '11', 11: '11'
}

waxing gibbous solverpython
from sage.all_cmdline import Matrix, vector, GF

moon_to_fixed_msb_precomp = {
    k: [
        (63 - idx, int(fix_bit)) for idx, fix_bit in enumerate(v)
        if fix_bit != "?"
    ]
    for k, v in moon_to_fixed_msb.items()
}

F = GF(2)

connect_to_challenge("waxing gibbous", "♈♉♊♋♌♍♎♏♐♑♒♓⛎")

for trial in range(50):
    print(f"trial {trial}")
    moons = get_challenge()
    ok = False

    for offset in range(64):
        system_mat = []
        system_vec = []
        math_random = iter(prng_states)

        for _ in range(offset):
            next(math_random)
        for _ in range(250 + 128):
            backup_prng = next(math_random)

        for moon in moons:
            moon_prng_state = next(math_random)
            for bit_pos, fix_value in moon_to_fixed_msb_precomp[moon]:
                system_mat.append(moon_prng_state.coef(bit_pos))
                system_vec.append(fix_value)

        try:
            s0s1 = Matrix(F, system_mat).solve_right(vector(F, system_vec))
            print(f"Found s0s1 with {offset = }")
        except ValueError:
            # no solution, offset is wrong
            continue

        math_random = iter(prng_states)
        def rng(n):
            return int(u64_to_f64(next(math_random).eval_all(s0s1)) * n)

        for _ in range(offset):
            next(math_random)
        backup = []
        for _ in range(250 + 128):
            backup.append(rng(12))

        soln = []
        for moon_idx in range(250 + 128):
            moon = rng(13)
            if moon == 12:
                moon = backup[moon_idx]
            if moon_idx >= 250:
                soln.append(moon)

        if answer_challenge(soln):
            ok = True
            break

    if not ok:
        raise ValueError("No solution found")

flag = claim_flag()

output

solving pow 6xsi10sC7B
 6xsi10sC7BQNV0Y6gP
trial 0
challenge: ♎♈♒♉♍♐♉♉♑♊♉♍♌♊♉♏♐♈♑♑
Found s0s1 with offset = 50
answer: ♎♉♊♉♒♓♌♌♌♏♋♉♐♎♉♐♊♑♎♓
trial 1
challenge: ♐♈♌♑♏♏♍♊♋♋♊♊♏♊♍♋♈♌♓♉
Found s0s1 with offset = 20
answer: ♎♓♊♋♏♉♒♒♎♎♒♏♍♊♊♋♈♌♐♊
trial 2
[...many lines...]
trial 49
challenge: ♒♋♎♈♓♋♏♌♒♏♌♋♐♈♐♍♉♏♌♋
Found s0s1 with offset = 11
Found s0s1 with offset = 12
answer: ♊♌♎♏♊♊♐♏♏♏♌♓♍♌♋♍♓♊♓♈
PCTF{i'd_be_very_impressed_and_sad_if_you_used_an_SMT_solver_ae21ef4bd0}

Also see imaginaryCTF 2022 challenge Poker

The Other CSS

By bluepichu, foxtrot and ubuntor

Long ago, I found a chest with some most curious booty: two pristine shiny disks, and a piece of parchment promisin’ me wealth and riches if I could reveal their secrets. Now, many years later, I’ve finally found a machine capable o’ gettin’ their data — but the scupperin’ thing jammed with one o’ me disks inside! Worse yet, the machine only be half o’ what I need: it acts as a “player” and needs some other device to act as “host” to communicate with it! Can ye help me out, bucko? (Note: PPP does not condone media piracy)

Attachment: the-other-css.tar.gz

We have a toy implementation of the Content Scramble System algorithm that is usually used to encrypt DVD data. This implementation has a expanded key size of 64 instead of 40 and more rounds in the mangle function.

Notably, the Cipher class is effectively a xorpad function that generates a bitstream from the given key and two LFSRs. Its encryption and decryption functions are equivalent, and knowing the xorpad is sufficient to obtain an encryption / decryption oracle with some key.

Disk A

The CSS_AUTHENTICATION_KEY, CSS_PLAYER_KEY_ID, and CSS_PLAYER_KEY_DATA are not given, nor is the keys file used when making the two disks. If you want to test locally, make your own disks and set your own keys. CSS_AUTHENTICATION_KEY is fixed and will not change. The flag is case insensitive.

nc the-other-css.chal.pwni.ng 1996

11 solves, 200 points

This sub-challenge involves exploiting the authentication handshake, then receiving and reading the data in a.disk.

Challenge css/player.py
python
host_challenge = await self._read_or_fail(rw, 16)
challenge_key = host_challenge[:8] # user controlled
encrypted_host_nonce = host_challenge[8:] # user controlled
cipher = Cipher(authentication_key, Mode.Authentication)
host_mangling_key = cipher.encrypt(challenge_key)
response = mangle(host_mangling_key, encrypted_host_nonce)
await self._write(rw, response)

We can query the server mutliple times to obtain y = mangle(Cipher(k) ^ a, b) where:

k is a server secret, and by extension Cipher(k) is unknown
a and b is user controlled
y is the retunred to the user

Challenge css/mangle.pypython
from .table import reverse_table, table

def mangle(key_bytes: bytes, value_bytes: bytes) -> bytes:
    key = list(key_bytes)
    value = list(value_bytes)

    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)

    return bytes(value)

def unmangle(key_bytes: bytes, value_bytes: bytes) -> bytes:
    key = list(key_bytes)
    value = list(value_bytes)

    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)
    value = unshift(value)
    value = untabulate(value)
    value = unmix(key, value)
    value = unshift(value)
    value = untabulate(value)
    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)

    return bytes(value)

def mix(key: list[int], value: list[int]) -> list[int]:
    last = 0
    ret: list[int] = value.copy()
    for i in range(len(value)):
        ret[i] ^= key[i]
        ret[i] ^= last
        last = value[i]
    return ret

def unmix(key: list[int], value: list[int]) -> list[int]:
    last = 0
    ret: list[int] = value.copy()
    for i in range(len(value)):
        ret[i] ^= last
        ret[i] ^= key[i]
        last = ret[i]
    return ret

def shift(value: list[int]) -> list[int]:
    ret = value.copy()
    ret[0] ^= ret[-1]
    return ret

unshift = shift

def tabulate(value: list[int]) -> list[int]:
    ret = value.copy()
    for i in range(len(value)):
        ret[i] = table[ret[i]]
    return ret

def untabulate(value: list[int]) -> list[int]:
    ret = value.copy()
    for i in range(len(value)):
        ret[i] = reverse_table[ret[i]]
    return ret
from .table import reverse_table, table


def mangle(key_bytes: bytes, value_bytes: bytes) -> bytes:
    key = list(key_bytes)
    value = list(value_bytes)

    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)

    return bytes(value)

def unmangle(key_bytes: bytes, value_bytes: bytes) -> bytes:
    key = list(key_bytes)
    value = list(value_bytes)

    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)
    value = unshift(value)
    value = untabulate(value)
    value = unmix(key, value)
    value = unshift(value)
    value = untabulate(value)
    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)
    value = unshift(value)
    value = unmix(key, value)

    return bytes(value)

def mix(key: list[int], value: list[int]) -> list[int]:
    last = 0
    ret: list[int] = value.copy()
    for i in range(len(value)):
        ret[i] ^= key[i]
        ret[i] ^= last
        last = value[i]
    return ret

def unmix(key: list[int], value: list[int]) -> list[int]:
    last = 0
    ret: list[int] = value.copy()
    for i in range(len(value)):
        ret[i] ^= last
        ret[i] ^= key[i]
        last = ret[i]
    return ret

def shift(value: list[int]) -> list[int]:
    ret = value.copy()
    ret[0] ^= ret[-1]
    return ret

unshift = shift

def tabulate(value: list[int]) -> list[int]:
    ret = value.copy()
    for i in range(len(value)):
        ret[i] = table[ret[i]]
    return ret

def untabulate(value: list[int]) -> list[int]:
    ret = value.copy()
    for i in range(len(value)):
        ret[i] = reverse_table[ret[i]]
    return ret

A careful symbolic implementation of mangle with z3 will succeed in calculating Cipher(k) ^ a and therefore Cipher(k) in around 3 minutes. Some implementation details used to speed up the solver include:

Use a 64-bit BitVec to represent intermediate states instead of a list of 8-bit BitVec. The mix function will be simpler for z3 to solve.
Select nonce bytes b that have low edit distance from each other. This will reduce diffusion of the nonce bytes after passing through substitution.
Implement the substitution step tabulate as a z3.Function; see the ACSC 2023 challenge SusCipher writeup by deuterium

Collect mangle datapython
from pwn import remote, context
context.log_level = "error"

def query(mangle_in):
    r = remote("the-other-css.chal.pwni.ng", 1996)
    # challenge key is null, mangle is low bits set
    r.sendline(bytes([0] * 8 + list(mangle_in)))
    res = r.recv(8)
    r.close()
    return list(res)

mangle_ins = [
    [0, 0, 0, 0, 0, 0, 0, 0],
    [1, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0],
    [0, 0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 1, 0, 0],
    [0, 0, 0, 0, 0, 0, 1, 0],
    [0, 0, 0, 0, 0, 0, 0, 1],
]

mangle_outs = [query(mangle_in) for mangle_in in mangle_ins]

for mangle_out in mangle_outs:
    print(mangle_out)

output

[240, 150, 0, 62, 234, 110, 177, 181]
[236, 247, 121, 13, 52, 60, 10, 181]
[240, 27, 101, 225, 163, 29, 157, 148]
[6, 96, 115, 108, 181, 159, 107, 22]
[16, 84, 34, 56, 198, 203, 125, 52]
[231, 148, 41, 2, 11, 205, 176, 200]
[44, 247, 96, 97, 104, 28, 81, 25]
[181, 239, 145, 180, 153, 58, 200, 107]
[7, 186, 235, 63, 143, 58, 177, 204]

Symbolic mangle functionspython
import z3
from css.table import table

def mix(key, value):
    ret = value ^ z3.LShR(value, 8) ^ key
    return ret

def shift(value):
    ret = value ^ (value << 56)
    return ret

def build_tabulate_one(solver):
    tabulate_one = z3.Function("tabulate", z3.BitVecSort(8), z3.BitVecSort(8))
    for idx, table_i in enumerate(table):
        solver.add(tabulate_one(idx) == table_i)
    return tabulate_one

def tabulate(value, name, tabulate_one, solver):
    value_sym = z3.BitVec(name, 64)
    solver.add(value_sym == value)
    ret = []
    for pos in reversed(range(0, 64, 8)):
        ret.append(tabulate_one(z3.Extract(pos+7, pos, value_sym)))
    ret = z3.Concat(*ret)
    return ret

def u8s_to_bitecval(x):
    return z3.BitVecVal(int(bytes(x).hex(), 16), len(x) * 8)

Break mangle to solve for Cipher(k)python
s = z3.Solver()

tabulate_one = build_tabulate_one(s)

key = z3.BitVec("key", 64)

for idx, (mangle_in, mangle_out) in enumerate(zip(mangle_ins, mangle_outs)):
    value = u8s_to_bitecval(mangle_in)
    goal = u8s_to_bitecval(mangle_out)

    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value, f"one_{idx}", tabulate_one, s)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value, f"two_{idx}", tabulate_one, s)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)

    s.add(value == goal)

print(s.check())

cipher_auth_key = hex(s.model()[key].as_long())[2:].zfill(16)
print(cipher_auth_key)

output

sat
0bfb91847347be4a

The xorpad generated by Cipher(k) can be calculated and can be reused for any calls to Cipher(k). This is sufficient to complete the handshake. The disk data can be streamed in and decrypted with keys obtained from the handshake to yield an .iso file which can be watched in VLC for the flag.

Perform handshakepython
from css.mangle import mangle

def bxor(a, b):
    return bytes([i ^ j for i, j in zip(a, b)])
def do_cipher_auth_key(x):
    k = bytes.fromhex(cipher_auth_key)
    return bxor(x, k)

r = remote("the-other-css.chal.pwni.ng", 1996)

host_challenge = bytes([0] * 16)
r.send(host_challenge)
challenge_key = host_challenge[:8]
encrypted_host_nonce = host_challenge[8:]
host_mangling_key = do_cipher_auth_key(challenge_key)

r.recv(8)

host_nonce = do_cipher_auth_key(encrypted_host_nonce)

player_challenge_key = r.recv(8)
encrypted_player_nonce = r.recv(8)
player_nonce = do_cipher_auth_key(encrypted_player_nonce)

player_mangling_key = do_cipher_auth_key(player_challenge_key)
response = mangle(player_mangling_key, do_cipher_auth_key(player_nonce))
r.send(response)

mangling_key = bxor(host_mangling_key, player_mangling_key)
session_nonce = bxor(host_nonce, player_nonce)
session_key = mangle(mangling_key, session_nonce)

Save disk datapython
from tqdm import tqdm
from itertools import count, cycle
from css.cipher import Cipher
from css.mode import Mode

sectors = []
for _ in tqdm(count()):
    ct = b""
    try:
        ct = r.recvn(8208, timeout=5)
        sectors.append(ct)
    except Exception:
        ct = r.recv()
        sectors.append(ct)
    if len(ct) != 8208:
        break

stream_cipher = Cipher(session_key, Mode.Data)
print(session_key.hex())

decrypted_sectors = []
for sector in tqdm(sectors):
    sector = stream_cipher.decrypt(sector)
    x, t = sector[:16], sector[16:]
    decrypted_sectors.append(bxor(cycle(x), t))

with open("diskA.iso", "wb") as f:
    for s in decrypted_sectors:
        f.write(s)

A full solve script can be found here.

Improved meet-in-the-middle search on mangle key

I learnt about this after the CTF ended. References 1 2 3 4

Another way to implement symbolic search for the mangle key would involve a meet in the middle strategy. mangle(key, pt) is calculated until immediately before the second call to tabulate and unmangle(key, ct) is calculated until immediately after the first call to tabulate. At this point, both value states should be equal for a valid key.

MITM symbolic manglepython
import z3
from css.mangle import mangle, mix, unmix, shift, unshift, table, reverse_table

ks = [ z3.BitVec(f"k{i}", 8) for i in range(8) ]
pts = [ z3.BitVec(f"pt{i}", 8) for i in range(8) ]
cts = [ z3.BitVec(f"ct{i}", 8) for i in range(8) ]

t = z3.Function("t", z3.BitVecSort(8), z3.BitVecSort(8))
rt = z3.Function("rt", z3.BitVecSort(8), z3.BitVecSort(8))

def tabulate(x):
    return [t(z3.simplify(i)) for i in x]
def untabulate(x):
    return [rt(z3.simplify(i)) for i in x]

def mangle_mitm(key, pts, cts):
    fwd = pts

    fwd = mix(key, fwd)
    fwd = shift(fwd)
    fwd = mix(key, fwd)
    fwd = shift(fwd)
    fwd = mix(key, fwd)
    fwd = tabulate(fwd)
    fwd = shift(fwd)
    fwd = mix(key, fwd)

    rev = cts
    rev = unmix(key, rev)
    rev = unshift(rev)
    rev = unmix(key, rev)
    rev = unshift(rev)
    rev = untabulate(rev)

    return fwd, rev

fwd_sym, rev_sym = mangle_mitm(ks, pts, cts)

On manual inspection, we can see that the intermediate state at bytes 0 and 7 only depend on key bytes appearing in 4 locations.

Inspect intermediate statepython
ef mitm_report(which):
    fwd_sym_str = str(fwd_sym[which])
    rev_sym_str = str(rev_sym[which])

    print(f"fwd[{which}] = (\n{fwd_sym_str}\n)")
    print(f"rev[{which}] = (\n{rev_sym_str}\n)")

python

mitm_report(0)

python

fwd[0] = (
    t(pt0 ^ k7 ^ pt6 ^ k6 ^ pt5 ^ k0) ^       # depends on k0/6/7
    t(pt7 ^ k6 ^ pt5 ^ k7 ^ pt6 ^ k5 ^ pt4) ^ # k5/6/7
    k0                                        # k0
)
rev[0] = (
    rt(k0 ^ ct7 ^ ct5 ^ ct3 ^ ct1 ^ k2 ^ k4 ^ k6 ^ ct0) # k0/2/4/6
)

python

mitm_report(7)

python

fwd[7] = (
    t(pt6 ^ k5 ^ pt4 ^ k6 ^ pt5 ^ k4 ^ pt3) ^ # k4/5/6
    t(pt7 ^ k6 ^ pt5 ^ k7 ^ pt6 ^ k5 ^ pt4) ^ # k5/6/7
    k7                                        # k7
)
rev[7] = (
    rt(ct6 ^ ct4 ^ ct2 ^ ct0 ^ k1 ^ k3 ^ k5 ^ k7) # k1/3/5/7
)

Instead of solving for all key bytes at the same time, we can choose to only solve for these 4 subsets of the key bytes, which is efffectively a 32-bit brute force that is completed quickly. This can be done by grouping the subsets of key bytes accordingly and only applying constraints on the one byte of intermediate state at a time. We can run this once for byte 0 and again for byte 7, after which key bytes 0/4/5/6/7 can be calculated and the remaining 3 bytes are easily brute forced.

An implementation of this search is available here.

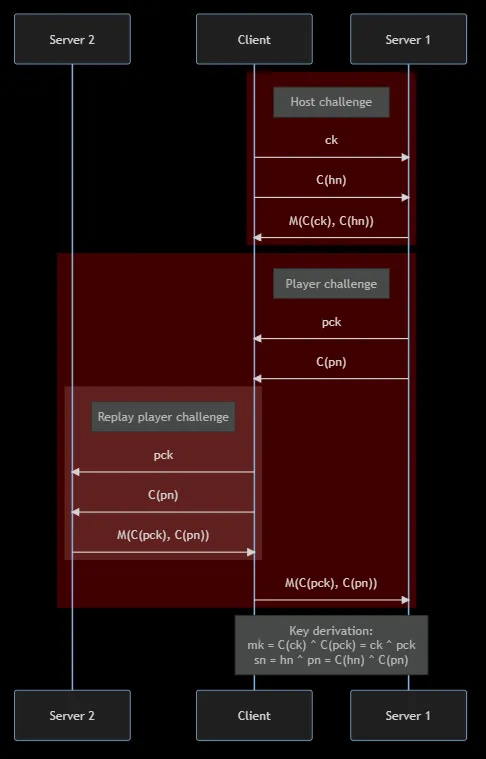
Unintended challenge reuse attack on handshake

I learnt about this after the CTF ended. References 1 2

Opening two simultaneous connections to the server and strategic use of the mangle(Cipher(k) ^ a, b) oracle is sufficient to pass the authentication check. We can forward the player challenge from the first connection as a host challenge to the second connection and will receive a valid response.

Because of how Cipher() functions as a xorpad, the xor of encrypted strings will produce the xor of the plaintext strings. This lets us regenerate the parameters used to derive session_key when downloading the disc contents.

Disk B

If your flag gets rejected, try adding an underscore between the first and second parts of the flag.

5 solves, 250 points

Since we have the full decryption of a.disk, we now need an offline method to decrypt b.disk. Looking at a.disk data, the xorpad used to encrypt each sector and the sector_nonce can be obtained.

Challenge css/player.py
python
sector_nonce = f.read(8)
if len(sector_nonce) == 0:
    break
sector_key = mangle(disk_key, sector_nonce)
sector_cipher = Cipher(sector_key, Mode.Data)
data = sector_cipher.decrypt(f.read(8208))
await self._write(rw, stream_cipher.encrypt(data))

We have multiple y = Cipher(mangle(k, n)), one for each sector in a.disk, where

y is a long bitstream derived from the two LFSR in Cipher
n is a nonce which is fixed from a.disk
k is the disk_key which we want to obtain

Challenge css/cipher.py
python
class Cipher:
    def __init__(self, key_bytes: bytes, mode: Mode):
        # ...
        key = int.from_bytes(key_bytes, "big")
        key_1 = (key & 0xffffff0000000000) >> 40
        key_2 = (key & 0x000000ffffffffff)
        lfsr_seed_1 = ((key_1 & 0xfffff8) << 1) | 8 | (key_1 & 7)
        lfsr_seed_2 = ((key_2 & 0xfffffffff8) << 1) | 8 | (key_2 & 7)
        self.lfsr_1 = LFSR(25, lfsr_seed_1, 0x19e4001) # replaces lsfr-17
        self.lfsr_2 = LFSR(41, lfsr_seed_2, 0xfdc0000001) # replaces lsfr-25

    def _get_lfsr_byte(self) -> int:
        byte_1 = self.lfsr_1.next_byte()
        byte_2 = self.lfsr_2.next_byte()
        # ...
        result = byte_1 + byte_2 + self.carry
        self.carry = (result >> 8) & 1
        return result & 0xff

For each sector, can use brute force to recover the key (mangle(k, n)) provided to Cipher. This can be efficiently done by first assuming the 24-bit value of key1, calculating the bitstream that would have come from lfsr2, and then verifying if this bitstream is could have come from a LFSR with taps 0xfdc0000001. If the stream is valid, the rest of key2 can be obtained by running the LFSR in reverse, thus regenerating the whole key. An optimized implementation of the LFSR allows one sector’s mangle(k, n) to be calculated in around 10 minutes.

Collect sector cipher streampython
from pwn import remote, context
from tqdm import tqdm
from itertools import count, cycle
from css.mangle import mangle
from css.cipher import Cipher
from css.mode import Mode

context.log_level = "error"

cipher_auth_key = "0bfb91847347be4a"

def bxor(a, b):
    return bytes([i ^ j for i, j in zip(a, b)])
def do_cipher_auth_key(x):
    k = bytes.fromhex(cipher_auth_key)
    return bxor(x, k)

# Do handshake

r = remote("the-other-css.chal.pwni.ng", 1996)

host_challenge = bytes([0] * 16)
r.send(host_challenge)
challenge_key = host_challenge[:8]
encrypted_host_nonce = host_challenge[8:]
host_mangling_key = do_cipher_auth_key(challenge_key)

r.recv(8)

host_nonce = do_cipher_auth_key(encrypted_host_nonce)

player_challenge_key = r.recv(8)
encrypted_player_nonce = r.recv(8)
player_nonce = do_cipher_auth_key(encrypted_player_nonce)

player_mangling_key = do_cipher_auth_key(player_challenge_key)
response = mangle(player_mangling_key, do_cipher_auth_key(player_nonce))
r.send(response)

mangling_key = bxor(host_mangling_key, player_mangling_key)
session_nonce = bxor(host_nonce, player_nonce)
session_key = mangle(mangling_key, session_nonce)

# Collect sector data including sectorxor

sectors = []
for _ in tqdm(range(10)):
    ct = b""
    try:
        ct = r.recvn(8208, timeout=5)
        sectors.append(ct)
    except Exception:
        ct = r.recv()
        sectors.append(ct)
    if len(ct) != 8208:
        break

stream_cipher = Cipher(session_key, Mode.Data)
print(session_key.hex())

decrypted_sectors_with_sector_xor = []
for sector in tqdm(sectors):
    decrypted_sectors_with_sector_xor.append(stream_cipher.decrypt(sector))

# Recover cipher xorpad stream

disk_a_ct = open("disks/a.disk", "rb")

sector_params = []
for sector_idx in range(10):
    disk_a_ct.seek(8 * 128 + sector_idx * (8208 + 8))
    sector_nonce = disk_a_ct.read(8)
    sector_ct = disk_a_ct.read(64)
    sector_pt = decrypted_sectors_with_sector_xor[sector_idx]
    sector_stream = bxor(sector_ct, sector_pt)

    sector_params.append({
        "idx": sector_idx,
        "nonce": sector_nonce.hex(),
        "stream": sector_stream.hex()
    })

print(f"{sector_params = }")

python

sector_params = [
    {'idx': 0,
    'nonce': 'a9debb718177adaa',
    'stream': '50cff4558f8195fbe907baf6480ca15306e5d55cc3f374e0de18dd3e6406d7a7295b3f18ef38d98a51b005f96924e4dde831d69b825139bff8fe1045ba42400e'},
    {'idx': 1,
    'nonce': '4911982d2aafef95',
    'stream': '2599656b5d11fc0fc8682471e676e437199fa8635ce869ef7f8ee678a3b39dca1a5cbd440c6d6464e8be712f959ff9a78241b7bc619b720dd4c3785085c9e0f8'},
    # [...more lines...]
    {'idx': 9,
    'nonce': '779ce5bbeda83fc0',
    'stream':
    '57a5f99b82b697684a540bd0fab3eda6e000ef82c3b9174ec94dafe623d4096dba150a8d1fba27b5aa5432a462ddb32a3d5f40e48ee8935bd3f1d8aa299d3adf'}
]

Search for LFSR key1python
from functools import lru_cache
from numba import jit
from numba.typed import List

cipher_nsamp = 16
stream_nsamp = 12

@lru_cache
def taps_to_tapmasks(taps):
    tapmasks = List()
    m = 1
    while taps:
        if m & taps:
            tapmasks.append(m)
            taps = taps ^ m
        m <<= 1
    return tapmasks

# Speed up LFSR with numba
@jit(nopython=True)
def fast_calc_lfsr_inner(size, seed, tapmasks, iters, flip):
    state = seed

    m = 1
    ret = 0
    rets = []
    for _ in range(iters):
        b = 0
        for tapmask in tapmasks:
            b ^= ((state & tapmask) == tapmask)
        state = (b << (size - 1)) | (state >> 1)

        b ^= flip
        ret = ret | (b * m)
        m <<= 1

        if m == 0x100:
            m = 1
            rets.append(ret)
            ret = 0

    if m != 1:
        rets.append(ret)

    return rets

def calc_lfsr(size, seed, taps, iters, flip):
    tapmasks = taps_to_tapmasks(taps)
    rets = fast_calc_lfsr_inner(size, seed, tapmasks, iters, flip)
    ret = 0
    for idx, i in enumerate(rets):
        ret += i << (idx * 8)
    return ret

def check_key1(key1, numall):
    seed1 = ((key1 & 0xfffff8) << 1) | 8 | (key1 & 7)
    num1 = calc_lfsr(25, seed1, 0x19e4001, stream_nsamp * 8, 1)
    num2 = (numall - num1) & ((1 << (stream_nsamp * 8)) - 1)
    head_key2 = (num2 & 0x1ffffffffff) ^ 0x1ffffffffff
    tail_num2 = calc_lfsr(41, head_key2, 0xfdc0000001, stream_nsamp * 8 - 41, 1)
    if tail_num2 == num2 >> 41:
        return key1
    return None

def keystream_to_numall(keystream):
    keystream = bytes.fromhex(keystream)[:cipher_nsamp]
    numall = int(bytes(keystream[::-1]).hex(), 16)
    return numall

def recover_key1(stream_idx, posthoc=None):
    numall = keystream_to_numall(sector_params[stream_idx]["stream"])
    start_from = 0 if posthoc is None else posthoc
    for i in tqdm(range(start_from, 0x1000000)):
        res = check_key1(i, numall)
        if res is not None:
            print("!!!", stream_idx, hex(res))
            return res
    return None

# posthocs = [None] * 10
posthocs = [
    0xd50000, 0x670000, 0xd10000, 0x200000, 0x810000,
    0x6c0000, 0xef0000, 0x6a0000, 0x460000, 0xfb0000,
]

for sector_param, posthoc in zip(sector_params, posthocs):
    sector_param["key1"] = recover_key1(sector_param["idx"], posthoc=posthoc)

output

!!! 1 0x677650
!!! 2 0xd127bb
!!! 3 0x2085ba
!!! 4 0x81201c
!!! 5 0x6c0b85
!!! 6 0xef36b7
!!! 7 0x6a9136
!!! 8 0x465aa9
!!! 9 0xfb01ac

Reverse LFSR to generate key2python
from css.lfsr import LFSR

def undo_lfsr(self):
    bit = self.state >> (self.size - 1)
    self.state = self.state ^ (bit << (self.size - 1))
    self.state = self.state << 1
    for tap in self.taps:
        bit ^= (self.state & tap) == tap
    self.state = self.state ^ bit

# Monkey patch the actual LFSR
LFSR.undo_lfsr = undo_lfsr

def generate_key2(stream_idx):
    key1 = sector_params[stream_idx]["key1"]
    numall = keystream_to_numall(sector_params[stream_idx]["stream"])
    seed1 = ((key1 & 0xfffff8) << 1) | 8 | (key1 & 7)
    num1 = calc_lfsr(25, seed1, 0x19e4001, stream_nsamp * 8, 1)
    num2 = (numall - num1) & ((1 << (stream_nsamp * 8)) - 1)
    head_key2 = (num2 & 0x1ffffffffff) ^ 0x1ffffffffff
    unlfsr2 = LFSR(41, head_key2, 0xfdc0000001)
    for _ in range(41):
        unlfsr2.undo_lfsr()
    lfsr_key2 = unlfsr2.state
    key2 = ((lfsr_key2 >> 1) & 0xfffffffff8) | (lfsr_key2 & 7)
    return key2

for sector_param, posthoc in zip(sector_params, posthocs):
    sector_param["key2"] = generate_key2(sector_param["idx"])
    sector_param["key"] = (
        hex(sector_param["key1"])[2:].zfill(6) +
        hex(sector_param["key2"])[2:].zfill(10)
    )
    print(sector_param["key"])

output

d58b0c1a3a08361c
677650352d147b20
d127bb11efa1b9b5
2085ba6294098918
81201c6acdd7e256
6c0b85ec94e8a9f0
ef36b7f5094b82e5
6a9136427269ab4f
465aa988c4a412fe
fb01ac777938dab9

After this, we obtain multiple values of y = mangle(k, n) with multiple sets of n and y and one shared unknown k. We can reuse the solution to Disk A and use z3 to solve for k. Because there is no control over n, the solver took around 30 minutes to complete.

Break mangle to solve for disk_keypython
import z3
from css.table import table

mangle_ins = []
mangle_outs = []
for sector_param in sector_params:
    mangle_ins.append(list(bytes.fromhex(sector_param["nonce"])))
    mangle_outs.append(list(bytes.fromhex(sector_param["key"])))

def mix(key, value):
    ret = value ^ z3.LShR(value, 8) ^ key
    return ret

def shift(value):
    ret = value ^ (value << 56)
    return ret

def build_tabulate_one(solver):
    tabulate_one = z3.Function("tabulate", z3.BitVecSort(8), z3.BitVecSort(8))
    for idx, table_i in enumerate(table):
        solver.add(tabulate_one(idx) == table_i)
    return tabulate_one

def tabulate(value, name, tabulate_one, solver):
    value_sym = z3.BitVec(name, 64)
    solver.add(value_sym == value)
    ret = []
    for pos in reversed(range(0, 64, 8)):
        ret.append(tabulate_one(z3.Extract(pos+7, pos, value_sym)))
    ret = z3.Concat(*ret)
    return ret

def u8s_to_bitecval(x):
    return z3.BitVecVal(int(bytes(x).hex(), 16), len(x) * 8)

s = z3.Solver()

tabulate_one = build_tabulate_one(s)

key = z3.BitVec("key", 64)

# posthoc, otherwise will take 30min
s.add(z3.Extract(31, 0, key) == 0xc348b1fb)

for idx, (mangle_in, mangle_out) in enumerate(zip(mangle_ins, mangle_outs)):
    value = u8s_to_bitecval(mangle_in)
    goal = u8s_to_bitecval(mangle_out)

    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value, f"one_{idx}", tabulate_one, s)
    value = shift(value)
    value = mix(key, value)
    value = tabulate(value, f"two_{idx}", tabulate_one, s)
    value = shift(value)
    value = mix(key, value)
    value = shift(value)
    value = mix(key, value)

    s.add(value == goal)

print(s.check())

disk_a_key_hex = hex(s.model()[key].as_long())[2:].zfill(16)
print(disk_a_key_hex)

output

sat
54e50074c348b1fb

Once k i.e. disk_key of a.disk is recovered, we can re-derive all player keys and use them to decode b.disk to get the final flag.

Decrypt b.diskpython
disk_a_key = bytes.fromhex(disk_a_key_hex)
with open("./disks/a.disk", "rb") as f:
    disk_a_key_enc = f.read(8)
player_key_xorpad = bxor(disk_a_key, disk_a_key_enc)
f = open("./disks/b.disk", "rb")
disk_b_key_enc = f.read(8)
disk_b_key = bxor(player_key_xorpad, disk_b_key_enc)

disk_key = disk_b_key
print(disk_key.hex())

outfile = open("./diskB.iso", "wb")

f.seek(8 * 128)
for sector_index in tqdm(count()):
    sector_nonce = f.read(8)
    if len(sector_nonce) == 0:
        break
    sector_key = mangle(disk_key, sector_nonce)
    sector_cipher = Cipher(sector_key, Mode.Data)
    data = sector_cipher.decrypt(f.read(8208))

    sector_xorpad = data[:16]
    sector_buf = data[16:]

    sector_pln = bxor(sector_buf, cycle(sector_xorpad))
    outfile.write(sector_pln)

output

11fe4f04a729a3e6

A full solve script can be found here