SekaiCTF 2023 Writeups
Changelog (last updated 2023-08-31)
Update 2023-08-31: Expanded on writeups for RandSubWare and Noisier CRC
Full solution notebooks are available here.
RandSubWare
By deut-erium
[Insert GPT-generated sampletext description here]
nc chals.sekai.team 3037Attachment: chall.py
6 solves, 498 points
First blood 🩸 at 5:36:07 from CTF start.
We get an encryption oracle of a toy substitution-permutation network cipher with a randomly generated S-box and need to obtain the first round key.
The 5 rounds in this SPN cipher is highly suspicious. It turns out that the small number of rounds means that differences in ciphertext are poorly diffused, making it vulnerable to a differential attack. We can analyze this by simulating encryption locally with a random S-box and key leaking intermediate SPN states at the end of each step. Using this, we can observe how a 1-block difference in plaintext is eventually spread across the ciphertext at each step.
Analyze diffusion
from randsubware import gen_pbox, gen_sbox, SPN import random from tqdm.auto import tqdm import numpy as np BOX_SIZE = 6 NUM_BOX = 16 ROUNDS = 5 TOTAL_SIZE = BOX_SIZE * NUM_BOX pbox = gen_pbox(BOX_SIZE, NUM_BOX) class MySPN(SPN): leak_steps_names = [ "Round 0: ct = pt", "Round 0: ct = ct ^ self.round_keys[0]", "Round 1: ct = self.sbox(ct)", "Round 1: ct = self.perm(ct)", "Round 1: ct ^= round_key", "Round 2: ct = self.sbox(ct)", "Round 2: ct = self.perm(ct)", "Round 2: ct ^= round_key", "Round 3: ct = self.sbox(ct)", "Round 3: ct = self.perm(ct)", "Round 3: ct ^= round_key", "Round 4: ct = self.sbox(ct)", "Round 4: ct = self.perm(ct)", "Round 4: ct ^= round_key", "Round 5: ct = self.sbox(ct)", "Round 5: ct ^= round_key", ] def encrypt_and_leak(self, pt): # Re-implement with leak at each step leak_steps = [] leak_steps.append(pt) ct = pt ^ self.round_keys[0] leak_steps.append(pt) for round_key in self.round_keys[1:-1]: ct = self.sbox(ct) leak_steps.append(ct) ct = self.perm(ct) leak_steps.append(ct) ct ^= round_key leak_steps.append(ct) ct = self.sbox(ct) leak_steps.append(ct) ct = ct ^ self.round_keys[-1] leak_steps.append(ct) return leak_steps def generate_one_block_difference_plaintexts(): # Both have same blocks 1-15 pt_head = random.randrange(0, 2**(TOTAL_SIZE - BOX_SIZE)) << BOX_SIZE # Both have different block 0 pt_a_tail, pt_b_tail = random.randrange(0, 2**BOX_SIZE), random.randrange(0, 2**BOX_SIZE) pt_a, pt_b = pt_head + pt_a_tail, pt_head + pt_b_tail return pt_a, pt_b n_iters = 25_000 samples = [] for _ in tqdm(range(n_iters)): # Randomly generated SPN sbox / key each time sbox = gen_sbox(BOX_SIZE) key = random.randrange(0, 2**TOTAL_SIZE) spn = MySPN(sbox, pbox, key, ROUNDS) # Make two plaintexts with only one block difference pt_a, pt_b = generate_one_block_difference_plaintexts() ct_a = spn.encrypt_and_leak(pt_a) ct_b = spn.encrypt_and_leak(pt_b) differential = [ i ^ j for i, j in zip(ct_a, ct_b) ] differential_bits = np.array([ [ int(j) for j in f"{i:096b}"[::-1] ] for i in differential ]) samples.append(differential_bits) # hack from https://stackoverflow.com/a/21009774 float_formatter = "{:.2f}".format np.set_printoptions(formatter={'float_kind':float_formatter}, linewidth=100) mean_differential = np.array(samples).mean(axis=0) mean_differential_2d = [] for step_name, differential in zip(MySPN.leak_steps_names, mean_differential): # print(f"mean different bits after {step_name}") differential_2d = differential.reshape((16, 6)).transpose() # print(differential_2d) mean_differential_2d.append((step_name, differential_2d))
Visualize diffusion
import seaborn as sns import matplotlib.pyplot as plt from matplotlib import animation heatmap_kwargs = { "cbar": False, "vmin": 0.0, "vmax": 1.0, "square": True, "annot": True, "fmt": ".2f", "cmap": "cividis" } ax_set_kwargs = { "xlabel": "block", "ylabel": "bit in block" } fig, ax = plt.subplots(1) fig.set_size_inches(9, 4) frame_data = ( mean_differential_2d[:1] + # Repeat the starting frame once mean_differential_2d + mean_differential_2d[-1:] * 2 # Repeat the ending frame twice ) zero_mat = np.zeros((6, 16)) def anim_init(): plt.title("", loc='left') ax.clear() sns.heatmap(zero_mat, **heatmap_kwargs) ax.set(**ax_set_kwargs) def anim_frame(i): step_name, data = frame_data[i] ax.clear() plt.title(f"Mean hamming distance of SPN state in 2 plaintexts with 1 block difference\n{step_name}", loc='left') sns.heatmap(data, **heatmap_kwargs) ax.set(**ax_set_kwargs) # Animate! anim = animation.FuncAnimation( fig, anim_frame, init_func=anim_init, frames=len(frame_data), repeat=False ) pillowwriter = animation.PillowWriter(fps=1) anim.save("randsubware.gif", writer=pillowwriter)
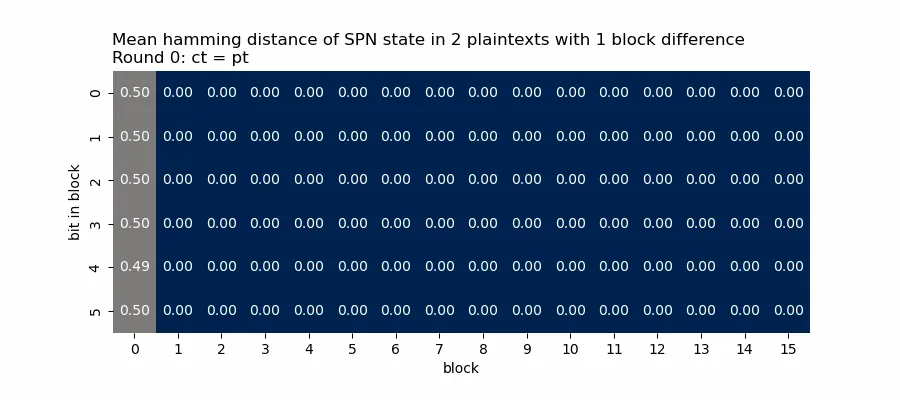
In a ct = sbox(ct) step any differential is “spread” across an entire block;
so long as any one bit in the block is different across two states the output of
the sbox will be very different. In a ct = pbox(ct) step the differences in
bits are rearranged around the SPN state. Any ct ^= round_key[i] step does not
affect the difference in states because a^b == (a^x)^(b^x).
For good SPN ciphers, changing one bit in the plaintext should change at least half of the bits in the ouput. However, in this toy SPN’s 4th round each bit in the state only has a 0.4 chance of being different across two inputs with one block difference. We can use this to our advantage in leaking the last round key.
The server oracle outputs the SPN state at the end of the 5th round. Firstly,
obtain some data by sending two plaintexts with only one block of difference.
The key idea is to guess the last round key and simulate the decryption
procedure just for the ct ^= round_key[5] and ct = ct.inv_sbox(ct) steps. If
we did guess the round key correctly, the two ciphertexts at that point should
follow a 0.4 chance of each bit being different and 0.6 chance of being equal.
If the key is incorrect, we have effectively applied another round of encryption
to the ciphertext and the probability of bits being different or equal should
both tend towards 0.5. The true key will likely be the one which has the
smallest hamming distance between partially decrypted ciphertexts.
By scaling up to 25k plaintext pairs and guessing the last round key one block at a time, we can efficiently and with good probability recover the correct last round key.
Query differential plaintext
from pwn import * from Crypto.Util.number import bytes_to_long r = remote("chals.sekai.team", 3037) r.recvuntil(b"sbox: ") sbox = list(bytes.fromhex(r.recvline().strip().decode())) spnkey = 0 # dummy key # local instance of SPN to help reversing steps spn = SPN(sbox, pbox, spnkey, 5) # Send differential inputs r.sendline(b"1") payload = [] for _ in range(n_iters): pt_a, pt_b = generate_one_block_difference_plaintexts() payload.append(f"{pt_a:012x}") payload.append(f"{pt_b:012x}") r.sendline("".join(payload).encode()) # Get differential outputs r.recvuntil(b"Quota remaining:") r.recvline() bulk_output = r.recvline().strip().decode() output_pairs = [] for i in range(0, len(bulk_output), 48): output_pairs.append(( bytes_to_long(bytes.fromhex(bulk_output[i:i+24])), bytes_to_long(bytes.fromhex(bulk_output[i+24:i+48])) ))
Solve for last round key
def solve_last_key(block_i): key_scores = [] # For each possible key for guess_key in range(64): # Total hamming distance across all pairs of differential ciphertexts total_distance = 0 for a, b in output_pairs: # Mask the selected block a_block = (a >> (block_i * 6)) & 63 b_block = (b >> (block_i * 6)) & 63 # Undo xorsub steps a_unxorsub = spn.SINV[a_block ^ guess_key] b_unxorsub = spn.SINV[b_block ^ guess_key] # Calculate hamming distance total_distance += (a_unxorsub ^ b_unxorsub).bit_count() key_scores.append((total_distance, guess_key)) # Find key with best fit key_scores.sort() print(f"Block {block_i:>2} candidates: {key_scores[:3]}") return key_scores[0][1] # Get the last key print() last_key = [] for block_i in tqdm(range(16)): last_key.append(solve_last_key(block_i)) print("last key blocks", last_key) last_key = int("".join(f"{i:06b}" for i in last_key[::-1]), 2) print("last key", last_key)
Block 0 candidates: [(73179, 44), (74083, 46), (74119, 63)] Block 1 candidates: [(73558, 31), (73798, 35), (73879, 50)] Block 2 candidates: [(73479, 9), (74058, 36), (74080, 21)] Block 3 candidates: [(73280, 47), (74117, 38), (74126, 35)] Block 4 candidates: [(73425, 6), (73964, 42), (73969, 51)] Block 5 candidates: [(73600, 62), (74003, 31), (74072, 43)] Block 6 candidates: [(73417, 1), (74151, 34), (74175, 23)] Block 7 candidates: [(73216, 36), (73877, 60), (74039, 55)] Block 8 candidates: [(73411, 16), (74016, 32), (74085, 44)] Block 9 candidates: [(73033, 26), (73953, 0), (73986, 36)] Block 10 candidates: [(73418, 8), (73769, 15), (74066, 14)] Block 11 candidates: [(73436, 9), (74152, 4), (74199, 23)] Block 12 candidates: [(73052, 37), (73842, 57), (73905, 24)] Block 13 candidates: [(73231, 58), (74190, 59), (74212, 9)] Block 14 candidates: [(73303, 21), (73809, 25), (74038, 15)] Block 15 candidates: [(73294, 32), (74027, 43), (74057, 60)] last key blocks [44, 31, 9, 47, 6, 62, 1, 36, 16, 26, 8, 9, 37, 58, 21, 32] last key 40037985158246157615730825196
Recover first round key
from randsubware import rotate_left first_key = last_key for _ in range(5): first_key = rotate_left( spn.inv_sbox(first_key), TOTAL_SIZE - BOX_SIZE - 1, TOTAL_SIZE ) print("first key", first_key) r.sendline(f"2\n{first_key}".encode()) print(r.recvuntil(b"}"))
first key 51786547602721728170223252735 b'Choose API option\n1. Test encryption\n2. Get Flag\n(int) key: SEKAI{d04e4ba19456a8a42584d5913275fe68c30893b74eb1df136051bbd2cd086dd0}'
Noisy CRC
By Utaha
I just learned that CRC can leak information about the original text, so I added noises to make it secure even if you can choose the generator polynomial! Good luck!
nc chals.sekai.team 3005Attachment: chall.py
49 solves, 244 points
We can choose a CRC16 polynomial and the server gives us the CRC of a secret number jumbled with 2 other random 16 bit integers. We aren’t allowed to send the same polynomial twice which prevents us from selecting numbers which appear twice. Identifying the secret number lets us decyrpt the flag.
Mathematically, CRC behaves like polynomials in , where the CRC of some ciphertext is the remainder of the ciphertext polynomial divided by the CRC polynomial. The oracle we are given is equivalent to for some fixed secret 1 and user-supplied modulus where .
To find which are the true CRCs among the noise, we want some way to tell if two different CRCs using different moduli came from the same source input. We can use a property of the modulo operation and think about using composite moduli. If we fix a small “integrity modulus” polynomial and vary a large polynomial such that has degree 16, two true CRCs taken residues modulo should be equal:
By querying with multiple CRC polynomials of this form, find the most common remainder when each of the CRCs are taken modulo . Any CRC which does not have this remainder must have been from random noise. After filtering, select the instances where only one candidate is left and this must be a true CRC. The secret can then be recovered using the chinese remainder theorem. We know we have the correct secret if the resulting polynomial from CRT only has coefficients up to . The flag can then be decrypted.
Query with integrity check
from pwn import * from tqdm.auto import tqdm Fn = GF(2) Rn.<x> = PolynomialRing(Fn) r = remote("chals.sekai.team", int(3005)) r.recvuntil(b"flag: ") flag_enc = r.recvline().strip().decode() def oracle_send(x): # helper to query with polynomial x = ZZ(list(x.change_ring(ZZ)), 2) r.sendline(f"{x}".encode()) def oracle_recv(): # helper to return polynomial r.recvuntil(b"ial: ") crcs = safeeval.expr(r.recvline()) crcs = [ Rn(ZZ(crc).bits()) for crc in crcs ] return crcs # Query 100 sets of g(x) * h_i(x) n = 100 integrity_modulus = x^4 + x + 1 assert integrity_modulus.is_irreducible() queries = [] while len(queries) < n: query = Rn.random_element(degree=12) # In case random_element collides if query not in queries: queries.append(query) oracle_send(query * integrity_modulus) results = [] for _ in tqdm(range(n)): results.append(oracle_recv())
Filter using integrity check
from collections import Counter from Crypto.Cipher import AES from hashlib import sha256 from Crypto.Util.number import long_to_bytes # Find the most common remainder when taken modulo integrity_modulus integrity_check_ctr = Counter([ j % integrity_modulus for i in results for j in i ]) top_three_integrity_remainders = integrity_check_ctr.most_common(3) print("top (s(x) % g(x), count):", top_three_integrity_remainders) integrity_remainder = top_three_integrity_remainders[0][0] print("using integrity remainder", integrity_remainder) # Most common residue must have appeared at least n times assert top_three_integrity_remainders[0][1] >= n assert top_three_integrity_remainders[1][1] < n # Recover CRT parts crt_res, crt_mod = [], [] for query, result in zip(queries, results): remainders_passing_integrity_check = [ result_i for result_i in result if result_i % integrity_modulus == integrity_remainder ] if len(remainders_passing_integrity_check) == 1: crt_res.append(remainders_passing_integrity_check[0]) crt_mod.append(query) print(f"Found {len(crt_mod)} remainder / moduli pairs passing integrity check") secret = CRT_list(crt_res, crt_mod) print(secret) secret = ZZ(list(secret.change_ring(ZZ)), 2) // 2^16 print(secret) cipher = AES.new( sha256(long_to_bytes(secret)).digest()[:16], AES.MODE_CTR, nonce=b"12345678" ) enc_flag = cipher.decrypt(bytes.fromhex(flag_enc)) print(enc_flag)
top (s(x) % g(x), count): [(x^3 + x^2, 113), (x^3 + x, 18), (x, 15)] using integrity remainder x^3 + x^2 Found 87 remainder / moduli pairs passing integrity check x^527 + x^524 + x^522 + x^521 + [...] + x^23 + x^21 + x^20 + x^19 + x^18 7959804053407355386545668333806001195256923739259240341029022811640181258258818922917787193638963987512949552561768678402333199293986084332025428172161468 b'SEKAI{CrCrCRcRCRcrcrcRCrCrC}'
Noisier CRC
By Utaha
I made a serious mistake last time. Now it won’t be that easy!
nc chals.sekai.team 3006Attachment: chall.py
8 solves, 495 points
There is a much better solution out there which doesn’t involve brute force, but this is what I managed during the CTF
We have a similar setup to Noisy CRC, but now:
- There are 12 extra random CRCs instead of 2 extra, for a total of 13 candidates per modulus.
- We must query with irreducible moduli, preventing us from using the “integrity check” strategy from earlier.
- Only 133 moduli can be queried.
To start with, since we can’t do much about the irreducible check just send 133 irreducible polynomials and obtain the noisy CRCs.
Query with irreducibles
from pwn import * from tqdm.auto import tqdm # context.log_level = "debug" Fn = GF(2) Rn.<x> = PolynomialRing(Fn) LOCAL = False r = remote("chals.sekai.team", int(3006)) # # Local instance with side channel leak for sanity checking # LOCAL = True # r = process(["python", "noisiercrc-localrun.py"]) r.recvuntil(b"flag: ") flag_enc = r.recvline().strip().decode() def oracle_send(x): # helper to query with polynomial x = ZZ(list(x.change_ring(ZZ)), 2) r.sendline(f"{x}".encode()) def oracle_recv(): # helper to return polynomial r.recvuntil(b"ial: ") crcs = safeeval.expr(r.recvline()) crcs = [ Rn(ZZ(crc).bits()) for crc in crcs ] return crcs # Query 133 sets of h_i(x) n = 133 queries = [] while len(queries) < n: query = Rn.irreducible_element(16, algorithm="random") # In case irreducible_element collides if query not in queries: queries.append(query) oracle_send(query) results = [] for _ in tqdm(range(n)): results.append(oracle_recv()) r.close()
Theoretically, combining the correct CRC samples with CRT will produce a short 527-degree polynomial despite 2128-degree modulus. Since CRT is a linear combination of remainders, we can transform all of the noisy CRCs into the polynomials that it would have contributed if it were included in CRT. We obtain 1729 different 2127-degree polynomials in 2. The sum of the correct 133 polynomials will correspond to the short secret polynomial which we want to recover. We can model this selection as one variable for each noisy CRC , which is if this polynomial is random noise and should not be selected or if this polynomial is a true CRC value and will contribute to the secret polynomial .
Raise with CRT
full_modulus = product(queries) noisy_polynomials = [] for crc_mod, crc_remainders in zip(queries, results): full_modulus_less_crc_mod = Rn(full_modulus // crc_mod) for crc_remainder in crc_remainders: noisy_polynomials.append(CRT(crc_remainder, 0, crc_mod, full_modulus_less_crc_mod)) if LOCAL: # Sanity check if running locally import json with open("noisiercrc-localrun-leak.json") as f: leak_data = json.load(f) leak_correct_polynomials = [idx * 13 + x for idx, x in enumerate(leak_data["correct_positions"])] leak_sum_of_correct_polynomials = sum([noisy_polynomials[i] for i in leak_correct_polynomials]) assert leak_sum_of_correct_polynomials.degree() <= 527
We know the secret should only have coefficients between and . Conversely, all other coefficents of the sum of valid CRCs should eventually be 0. Using these known zeros, we can seperate the equation above for each power of turn this into a system of 1616 equations ( powers of ) with 1729 unknowns ( individual ).
We have more unknowns than relationships, so there will be multiple solutions, to be exact up to of them. Sagemath lets us calculate the right kernel of the coefficient matrix; any solution must therefore lie in the lattice formed by the basis of this kernel.
Basis lattice
n_coeffs = full_modulus.degree() coeff_matrix = [] for noisy_polynomial in tqdm(noisy_polynomials): noisy_coeffs = list(noisy_polynomial) noisy_coeffs += [0] * (n_coeffs - len(noisy_coeffs)) coeff_matrix.append(noisy_coeffs) # One column = one polynomial, one row = one coefficient coeff_matrix = Matrix(Fn, coeff_matrix).transpose() force_zero_indices = list(range(0, 16)) + list(range(16 + 512, n_coeffs)) force_zero_goal = vector([0] * len(force_zero_indices)) basis = coeff_matrix[force_zero_indices].right_kernel().basis() basis_mat = Matrix(basis) print(repr(basis_mat)) import seaborn as sns import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(1729 / 50, 113 / 50)) sns.heatmap( Matrix(basis).numpy().astype(int), xticklabels=False, yticklabels=False, cbar=False )
113 x 1729 dense matrix over Finite Field of size 2

Fortunately, we don’t need to iterate through all possibilities. We know that the true combination of CRCs only involve 1 in every 13 noisy CRCs, and this corresponds to some linear combination of the basis vectors which has a low (but non-zero) hamming weight.
We can use this restriction to prune the search. See the nice diagonal of the basis lattice? If we guess the first 7-8 true CRCs from their groups of 13 noisy CRCs, we can use the sum of the corresponding basis vectors in the diagonal part of the basis to fix these bits. For any other rows that have high hamming weight but are not included in the diagonal, brute force the addition of all subsets of them. When any resultant combination has a low hamming weight, this is a possible solution.
Estimating bruteforce parameters
n_ident = None for d in range(80, 112): if basis_mat[:d, :d] == Matrix.identity(d): n_ident = d print(f"{n_ident=}") basis_mat_colsum = sum(basis_mat.change_ring(ZZ).columns()) highweights = [] for d in range(n_ident, 112): if basis_mat_colsum[d] > 40: highweights.append(d) print(f"{highweights=}") n_fix = n_ident // 13 n_tail = ZZ(n_ident % 13) estimated_bruteforce = 13^n_fix * (n_tail + 1) * 2^len(highweights) print(f"{estimated_bruteforce=} ({estimated_bruteforce.nbits()} bit)")
n_ident=93 highweights=[] estimated_bruteforce=188245551 (28 bit)
Brute force for short vector
from gmpy2 import mpz import itertools from multiprocessing import Pool basis_mpz = [ mpz("".join([str(i) for i in basis_row][::-1]), 2) for basis_row in basis ] fix_groups = [] for fix_group_i in range(n_fix): fix_group = basis_mpz[13*fix_group_i:13*(fix_group_i+1)] fix_groups.append(fix_group) tail_group = [mpz(0)] + basis_mpz[13*n_fix:13*n_fix+n_tail] highweight_group = [mpz(0)] for highweight_row in highweights: highweight_group = highweight_group + [ x ^^ basis_mpz[highweight_row] for x in highweight_group ] def xor_hamming_weight(x): a = mpz(int(0)) for i in x: a = a ^^ i res = bin(a).count("1") if res < 400: return res, x else: return None search_space = fix_groups + [tail_group, highweight_group] found_solns = [] with Pool(16) as pool: for res in tqdm( pool.imap_unordered(xor_hamming_weight, itertools.product(*search_space), chunksize=100000), total=int(estimated_bruteforce) ): if res is None: continue print(res) found_solns.append(res[1])
(134, (mpz(1682891056205077954240730947014674[...]2567431504905514254336), mpz(0), mpz(0)))
With this possible solution, throw away any groups of 13 noisy CRCs which have more than one CRC selected; the remainder will all correspond to the true CRCs. All that is left is to decrypt the flag.
Recover secret
from Crypto.Cipher import AES from hashlib import sha256 from Crypto.Util.number import long_to_bytes x = found_solns[0] a = mpz(0) for i in x: a = a ^^ i crt_res, crt_mod = [], [] for batch_i, (crc_mod, crc_remainders) in enumerate(zip(queries, results)): candidate_remainders = [] for pos in range(13): if a.bit_test(batch_i * 13 + pos): candidate_remainders.append(crc_remainders[pos]) if len(candidate_remainders) == 1: crt_res.append(candidate_remainders[0]) crt_mod.append(crc_mod) print(f"Found {len(crt_mod)} remainder / moduli pairs passing hamming weight check") secret = CRT_list(crt_res, crt_mod) print(secret) secret = ZZ(list(secret.change_ring(ZZ)), 2) // 2^16 print(secret) cipher = AES.new( sha256(long_to_bytes(secret)).digest()[:16], AES.MODE_CTR, nonce=b"12345678" ) enc_flag = cipher.decrypt(bytes.fromhex(flag_enc)) print(enc_flag)
Found 132 remainder / moduli pairs passing hamming weight check x^525 + x^524 + x^522 + x^521 + [...] + x^24 + x^22 + x^20 + x^19 + x^17 + x^16 2861996669066233382642628999080397198682644917269167528027115837487932896047094443906219867598067989713723341598622466499556971616571895239468302407679835 b'SEKAI{4R3_Y0U_cRc_M4s73R?}'
Thanks, I hate CRC now.
Intended solution using combinatoric linearisation
I learnt about this after the CTF ended. References 1
When modelling the selection problem earlier, we used 1729 variables to model if some polynomial is selected or should be ignored, creating 13 unknowns per set of noisy CRCs collected. We can reduce our solution space by instead “assuming” the first polynomial is the true CRC and then create 12 other choices that each “unselects” the first polynomial and introduces some other polynomial as the true CRC, encoded by a new variable we can call .
This way, we have encoded the 13 possible selections of the true CRC only using 12 variables. If we obtain a solution where , this means that the -th CRC is a true CRC. If all of for some fixed , this means that the first CRC was the true CRC since we did not “swap” out the original solution.
Using this compression of the combinatoric problem, we now have variables across relations and can efficiently solve this system of equations, though a trivial amount of brute force over the kernel of the coefficient matrix may still be required.
Combining this with the focused brute force approach from earlier, author Utaha says that the minimum queries required can drop to around 103 queries. In my limited testing I’ve found that this is possible with 101 queries and 32 bit brute force if you’re lucky.
For another challenge about linearisation, see imaginaryCTF 2023 Flagtor.
Diffecientwo
By deut-erium
Welcome to the Diffecientwo Caching Database API for tracking and storing content across social media. We have repurposed our security product, as saving the admin key was probably not the best idea.
We have decided to change our policies and to achieve better marketing, we are offering free API KEY to customers sharing #SEKAICTF #DEUTERIUM #DIFFECIENTWO #CRYPTO on LonelyFans (our premium business partner).
nc chals.sekai.team 3000Attachment: diffecientwo.py
13 solves, 484 points
A server implements a bloom filter with murmurhash3 using fixed known seeds of
0-63. We can add 22 new items of at most length 32 to the bloom filter and need
to manipulate the bloom filter such that the length 42 magic string
#SEKAICTF #DEUTERIUM #DIFFECIENTWO #CRYPTO is in the filter.
We want to generate some messages which when passed throught the bloom filter
collide with at least 33 of the hashes derived from the magic string. We can
try to cause this collision by solving for inputs using z3. One key observation
for speedup is to only constrain collisions only immediately after the
xor length operation in murmurhash3 as the bit shift operations after that are
not easily invertible.
Symbolic mmh3
import random import z3 def chunk(x, bs=4): return [ x[i:i+bs] for i in range(0, len(x), bs) ] # ====================== pure impl ====================== def mask(x, m=0xffffffff): return x & m def rotl32(x, n): return mask((x << n) | (x >> (32-n))) def mmh3_block(h, data): k = data k = mask(k * 0xcc9e2d51) k = rotl32(k, 15) k = mask(k * 0x1b873593) h = h ^ k h = rotl32(h, 13) h = mask(h * 5 + 0xe6546b64) return h def mmh3_tail(h, tail): k = tail k = mask(k * 0xcc9e2d51) k = rotl32(k, 15) k = mask(k * 0x1b873593) h = h ^ k return h def mmh3_addlen(h, total_len): return h ^ total_len def mmh3_finalize(h): h = h ^ (h >> 16) h = mask(h * 0x85ebca6b) h = h ^ (h >> 13) h = mask(h * 0xc2b2ae35) h = h ^ (h >> 16) return h def mmh3(data, tail=None, tail_len=0, seed=0x0): if isinstance(data, bytes): data = chunk(data) if len(data[-1]) != 4: data, tail = data[:-1], data[-1] tail_len = len(tail) data = [ int.from_bytes(data_i, "little") for data_i in data ] if tail is not None: tail = int.from_bytes(tail, "little") trace = { "blocks": [], "tail": None, "addlen": None, "final": None } total_len = len(data) * 4 + tail_len cur_hash = seed for data_i in data: cur_hash = mmh3_block(cur_hash, data_i) trace["blocks"].append(cur_hash) if tail is not None: cur_hash = mmh3_tail(cur_hash, tail) trace["tail"] = cur_hash cur_hash = mmh3_addlen(cur_hash, total_len) trace["addlen"] = cur_hash cur_hash = mmh3_finalize(cur_hash) trace["final"] = cur_hash return trace # ====================== symbolics ====================== def rotl32_sym(x, n): new_left, new_right = z3.Extract(31-n, 0, x), z3.Extract(31, 31-n+1, x) return z3.Concat(new_left, new_right) def mmh3sym_block(h, data): k = data k = k * 0xcc9e2d51 k = rotl32_sym(k, 15) k = k * 0x1b873593 h = h ^ k h = rotl32_sym(h, 13) h = h * 5 + 0xe6546b64 return h def mmh3sym_tail(h, tail): k = tail k = k * 0xcc9e2d51 k = rotl32_sym(k, 15) k = k * 0x1b873593 h = h ^ k return h def mmh3sym_addlen(h, total_len): return h ^ total_len def mmh3sym_finalize(h): h = h ^ z3.LShR(h, 16) h = h * 0x85ebca6b h = h ^ z3.LShR(h, 13) h = h * 0xc2b2ae35 h = h ^ z3.LShR(h, 16) return h def mmh3sym(data, tail=None, tail_len=0, seed=0x0, solver=None): nonce = random.randbytes(8).hex() def save_bv(suffix, eqn): new_bv = z3.BitVec(f"mmh3_{nonce}_{suffix}", 32) solver.add(new_bv == eqn) return new_bv trace = { "blocks": [], "tail": None, "addlen": None, "final": None } total_len = len(data) * 4 + tail_len cur_hash = seed for i, data_i in enumerate(data): cur_hash = mmh3sym_block(cur_hash, data_i) cur_hash = save_bv(f"b{i}", cur_hash) trace["blocks"].append(cur_hash) if tail is not None: cur_hash = mmh3sym_tail(cur_hash, tail) cur_hash = save_bv("t", cur_hash) trace["tail"] = cur_hash cur_hash = mmh3sym_addlen(cur_hash, total_len) cur_hash = save_bv("l", cur_hash) trace["addlen"] = cur_hash cur_hash = mmh3sym_finalize(cur_hash) cur_hash = save_bv("f", cur_hash) trace["final"] = cur_hash return trace
Obtain preimage
magic = b"#SEKAICTF #DEUTERIUM #DIFFECIENTWO #CRYPTO" addlen_goals = [] for seed in range(0, 64): addlen_goals.append((seed, mmh3(magic, seed=seed)["addlen"])) print(addlen_goals)
[(0, 2538403748), (1, 2698667000), (2, 2611445724), [...], (62, 2779364044), (63, 3988978496)]
z3 for collision
from multiprocessing import Pool from tqdm.auto import tqdm def solve_slice(addlen_slice): s = z3.Solver() n_chunks = 6 d_chunks = [z3.BitVec(f"d{i}", 32) for i in range(n_chunks)] for j, (_, addlen) in enumerate(addlen_slice): # print(f"Solving seed={j} => addlen={addlen}") s.add(mmh3sym(d_chunks, seed=j, solver=s)["addlen"] == addlen) if str(s.check()) != "sat": return [i[0] for i in addlen_slice], "err" m = s.model() d_hex = "".join([m[i].as_long().to_bytes(4, "little").hex() for i in d_chunks]) return [i[0] for i in addlen_slice], d_hex collisions = [] with Pool(16) as p: slices = chunk(addlen_goals, 3) for res in tqdm(p.imap_unordered(solve_slice, slices), total=len(slices)): collisions.append(res) print(res)
([15, 16, 17], '42cef17b4ab3914caa86fcd4132bcffe03034c0fd3cd151c') ([21, 22, 23], 'c7915c2ec5f0db9d427b05c9c90fae0feb40d40be24b3dd0') ([45, 46, 47], '0643d2cfb6b85605b114b34b54af84ed155b684ce487ec2c') ([30, 31, 32], '6b86b777986f37df94e9c10aa3dc4b55cd7ccd032c86a207') ([24, 25, 26], '49fc091621b7060584547b341b6975444d979c1181a25ae7') ([0, 1, 2], 'ebdbe651d60a7cc3a42cbb26448e587aab494e6b0cd98a26') ([63], 'ce55c8f2061a0a3bcd32f20b2711dcd1d5b3ce62f4bb4897') ([36, 37, 38], '99d06c7fb227fd3dd553532f31c268578e4b96761c510d9e') ([9, 10, 11], '98eff98f0bac953b92e337153fbcd4ab5e301226a7ce663f') ([3, 4, 5], '13a180bb5c26510922eb0af67841ba40dd3559bdf2ff20ea') ([6, 7, 8], '64e17ffd878c46d812617ea61e9edd1a1363f5e73bb047e9') ([39, 40, 41], 'fc1b50b8727c1ba1cb920804801d2a46d9f1eef72ad7d433') ([33, 34, 35], '6f6a24b7ee163935c1f48aecf1396e67af96506985245acf') ([54, 55, 56], 'fe32ca63e9d2a3a737ef462aa3e7955fe059c1aac1cbb0cf') ([51, 52, 53], '9677651246c8bace2dcba8a25206aea221f676033e0a0893') ([18, 19, 20], '221472f37a1bf41dd834d48edbdc06c0f7114d11bbc002c6') ([57, 58, 59], 'fe30b5177fb89866e513ceb798d6bd871c607f88a87156a8') ([42, 43, 44], '7b883b7441140a34d02d2305ec57ff1dc4f83cd947692375') ([12, 13, 14], 'cab82d6d2af0a11595aabd6b29b849873259740878f1c158') ([60, 61, 62], '56ad79ed9a3628a339102f487926486c71b070fa4c6605c8') ([27, 28, 29], '8bacbfbddbb20879fdf3425d4c5918c98949096f2bbcfa47') ([48, 49, 50], '019b3cbb4f85ee53ca123052f11d892442d58a524dfd949f')
Claim flag
from pwn import * payload = [] for _, i in collisions: payload.append("2") payload.append(i) payload.append("3") payload = "\n".join(payload) r = remote("chals.sekai.team", 3000) r.sendline(payload.encode()) r.recvuntil(b"}").rpartition(b"\n")[2]
b"b'SEKAI{1c8d8986a4c530225cb7711c4064dd63f19350ebdc46a250b9a8af16893203d8}"
cryptoGRAPHy 1
By sahuang
Graphs have gained an increasing amount of attention in the world of Cryptography. They are used to model many real-world problems ranging from social media to traffic routing networks. Designing a secure Graph Encryption Scheme (GES) is important as querying plaintext graph database can leak sensitive information about the users.
In this challenge I have implemented a novel GES. Please help me verify if the cryptosystem works.
Note:
lib.zipremains unchanged in this series. The flag for this challenge will be used to access the next one when unlocked.
nc chals.sekai.team 3001Attachment: lib.zip > server.py
76 solves, 100 points
The source code given is quite dense, but what matters is that we are given some
sort of AES key at the start and asked to obtain information from some
ciphertext. Reading the source tells us we need to use the front 16 bytes of the
key and then decyrpt chunks of the ciphertext 32 bytes at a time using the
provided utils.SymmetricDecrypt. This reveals information about the IDs of the
nodes visited in order.
Decrypt path with key
from pwn import * from libgraph import utils from tqdm.auto import tqdm r = remote("chals.sekai.team", 3001) r.recvuntil(b"Key: ") sk = bytes.fromhex(r.recvline().strip().decode()) sk_ske, sk_des = sk[:16], sk[16:] def do_round(): r.recvuntil(b"/50: ") # Pull starting node ID in plaintext src, _ = [int(i) for i in r.recvline().strip().decode().split()] r.recvuntil(b"Response: ") response_full = bytes.fromhex(r.recvline().strip().decode()) path = [src] for i in range(0, len(response_full), 32): # Decrypt next node ID in path step_tuple = utils.SymmetricDecrypt(sk_ske, response_full[i:i+32]) step_tuple = [int(i) for i in step_tuple.decode().split(",")] path += [step_tuple[0]] r.sendline(" ".join(str(i) for i in path).encode()) for _ in tqdm(range(50)): do_round() print(r.recvuntil(b"}"))
b'> Original query: [+] Flag: SEKAI{GES_15_34sy_2_br34k_kn@w1ng_th3_k3y}'
cryptoGRAPHy 2
By sahuang
I am wondering what can be leaked in my GES. Let me know if you can recover the graph structure in an Honest-But-Curious setting.
Note:
lib.zipremains unchanged in this series. The flag for this challenge will be used to access the next one when unlocked.
nc chals.sekai.team 3062Attachment: server.py
55 solves, 176 points
We can query with a start node and end node and are given the “tokens” of each node on the way to destination. The challenge wants us to reproduce the “node degrees in the single-destination shortest path tree”.
Query the paths of each starting node to the fixed destination node, generate a list of edges connecting adjacent tokens in all paths and re-build a “tree of tokens” (instead of tree of node IDs) with this edge list. Finally calculate the degree of each node and sort accordingly.
Calculate degree with tokens
from pwn import * from tqdm.auto import tqdm r = remote("chals.sekai.team", 3062) r.sendline(b"SEKAI{GES_15_34sy_2_br34k_kn@w1ng_th3_k3y}") def do_round(): # Recieve destination r.recvuntil(b"Destination: ") dst = int(r.recvline().strip().decode()) # Query all paths from * -> destination for i in range(130): if i == dst: continue r.sendline(f"{i},{dst}".encode()) # Recover adjacency lists token_adj = defaultdict(set) for i in range(130): if i == dst: continue r.recvuntil(b"Token: ") token = r.recvline().strip().decode() r.recvuntil(b"Query Response: ") trace = r.recvline().strip().decode() trace = trace[:64] token_adj[token].add(trace) token_adj[trace].add(token) # Calculate degrees proof = " ".join([str(i) for i in sorted([len(i) for i in token_adj.values()])]) r.sendline(f"-1,-1\n{proof}".encode()) for _ in tqdm(range(10)): do_round() print(r.recvuntil(b"}"))
b'> Query u,v: [!] Invalid query!\n> Answer: [+] Flag: SEKAI{3ff1c13nt_GES_4_Shortest-Path-Queries-_-}'
cryptoGRAPHy 3
By sahuang
Here is the hardest part: Can you directly recover the shortest path query if you are the server, having access to the original graph and all queries? (On a side note, this setting is somewhat realistic in scenarios such as Google Maps, where the whole routing map is available to the adversary.)
Note:
lib.zipremains unchanged in this series. This is the last challenge.
nc chals.sekai.team 3023Attachment: server.py
31 solves, 400 points
We are given an edge list with original node IDs of a tree graph, all the lists of tokens for all possible shortest paths in a tree graph and need to find a way to map tokens back to their original node ID.
For each shortest path, the last 32-byte token uniquely identifies the “single source” of the shortest path. We can group all of the shortest paths using by the “single source token”, then reconstruct the tree graph like in part 2 to obtain 60 different trees. All of these trees represent the same tree but with different a different root. We now need to find a way to convert trees with different root to the original node IDs.
Save original tree and group by family
from pwn import * r = remote("chals.sekai.team", 3023) r.sendline(b"SEKAI{3ff1c13nt_GES_4_Shortest-Path-Queries-_-}") r.send(b"1\n2\n") # Original edge list r.recvuntil(b"Edges: ") edges = safeeval.expr(r.recvline().strip().decode()) # All token shortest paths r.recvuntil(b"Query Responses: \n") apsp_tokens = r.recvuntil(b"============ MENU ============").strip().decode() apsp_tokens = apsp_tokens.split("\n")[:-1] # Map of family to adjacency lists # graphs[graph_family][a] = set(nodes connected to a) graphs = defaultdict(lambda: defaultdict(set)) for src, dst in edges: graphs["original"][src].add(dst) graphs["original"][dst].add(src) # For all paths, group by family for tokens_resp in apsp_tokens: tokens, _resp = tokens_resp.split(" ") # We can throw away resp tokens = chunk(tokens) family = tokens[-1] # Each tree is uniquely identified by the last token # Recover edge list for src, dst in zip(tokens, tokens[1:]): graphs[family][src].add(dst) graphs[family][dst].add(src)
First, find a node that can be uniquely identified from the tree structure, such as selecting the node with largest out-degree (and/or reconnecting until there is only 1 such node). Next, re-root each tree at that unqiue node. Ensure children are visited in the same order by implementing some kind of subtree hash function4. Repeat this one last time using the edge list given at the start. All the trees will now have the same structure and we can map tokens to original node IDs by finding its path from root (e.g. using preorder).
Re-root trees
from tqdm.auto import tqdm def get_nodes_of_max_degree(g): maximal_degree = max(len(v) for v in g.values()) nodes_with_maximal_degree = [k for k, v in g.items() if len(v) == maximal_degree] return nodes_with_maximal_degree # Ensure we have 1 unique node to root with assert len(get_nodes_of_max_degree(graphs["original"])) == 1 def chunk(x, bs=64): return [ x[i:i+bs] for i in range(0, len(x), bs) ] def root_graph(g): root_node = get_nodes_of_max_degree(g)[0] # children[node] = [children sorted by subtree hash] children = {} # DFS and return subtree hash, while building children def dfs1(node): children[node] = [] children_hashes = [] for other in g[node]: if other in children: # Already visited, skip continue children_hashes.append((dfs1(other), other)) if len(children_hashes) == 0: return "()" # leaf case children_hashes.sort() # Sort children by subtree hash own_hash, children[node] = list(zip(*children_hashes)) # Ensure children's subtrees are unique, otherwise the tree cannot be uniquely rooted assert len(set(own_hash)) == len(own_hash) # Calculate subtree hash, thankfully only 60 nodes in this tree # so we can abuse strings # https://codeforces.com/blog/entry/101010 return "(" + "".join(own_hash) + ")" dfs1(root_node) # Recover preorder preorder = 0 node_to_preorder = {} def dfs2(node): nonlocal preorder node_to_preorder[node] = preorder preorder += 1 for child in children[node]: dfs2(child) dfs2(root_node) return node_to_preorder # family_nodeid_to_preorder[family][token] = preorder when re-rooted family_token_to_preorder = {} for family in tqdm(graphs): family_token_to_preorder[family] = root_graph(graphs[family]) preorder_to_nodeid = {v: k for k, v in family_token_to_preorder["original"].items()}
Recover original node IDs
def do_round(): r.recvuntil(b"Token: ") token = r.recvline().strip().decode() r.recvuntil(b"Query Response: ") trace = r.recvline().strip().decode() parts = chunk(token + trace[:len(trace)//2]) family = parts[-1] steps = [] for part in parts: steps.append(preorder_to_nodeid[family_token_to_preorder[family][part]]) ans = " ".join(str(i) for i in steps) r.sendline(ans.encode()) r.sendline(b"3") for _ in tqdm(range(10)): do_round() print(r.recvuntil(b"}"))
b'> Original query: [+] Flag: SEKAI{Full_QR_Attack_is_not_easy_https://eprint.iacr.org/2022/838.pdf}'