SECCON CTF 2022 Crypto Writeups

Changelog (last updated 2022-11-20)

Update 2022-11-20: Added inequality-CVP solution for this_is_not_lsb along with some typos.

janken vs kurenaif
witches_symmetric_exam
insufficient
this_is_not_lsb
BBB
pqpq

janken vs kurenaif

By theoremoon

Do you know about the crypto witch? And about a her special cast too?

nc janken-vs-kurenaif.seccon.games 8080

Attachments: server.py

17 solves, 221 points

Challenge problem.pypython
import os
import signal
import random
import secrets

FLAG = os.getenv("FLAG", "fake{cast a special spell}")


def janken(a, b):
    return (a - b + 3) % 3

signal.alarm(1000)
print("kurenaif: Hi, I'm a crypto witch. Let's a spell battle with me.")

witch_spell = secrets.token_hex(16)
witch_rand = random.Random()
witch_rand.seed(int(witch_spell, 16))
print(f"kurenaif: My spell is {witch_spell}. What about your spell?")

your_spell = input("your spell: ")
your_random = random.Random()
your_random.seed(int(your_spell, 16))

for _ in range(666):
    witch_hand = witch_rand.randint(0, 2)
    your_hand = your_random.randint(0, 2)

    if janken(your_hand, witch_hand) != 1:
        print("kurenaif: Could you come here the day before yesterday?")
        quit()

print("kurenaif: Amazing! Your spell is very powerful!!")
print(f"kurenaif: OK. The flag is here. {FLAG}")

The challenge server seeds a python PRNG witch_rand and publishes the key, then asks for a user seed for another PRNG your_random. The two PRNGs then play rock-paper-scissors against each other. Our PRNG needs to play winning moves 666 times in a row to get the flag.

Since we know the witch_rand seed, first predict the 666 witch_rand results by making a copy of the PRNG on our local machine and then calculate what are the winning hands that your_random needs to produce.

Simulate PRNG locallypython
import random
from pwn import *

context.log_level = "error"

r = remote("janken-vs-kurenaif.seccon.games", 8080)
r.recvuntil(b"My spell is ")
witch_spell = r.recvuntil(b".")[:-1].decode()

witch_rand = random.Random()
witch_rand.seed(int(witch_spell, 16))

witch_hands = []
your_hands = []

for _ in range(666):
    witch_hand = witch_rand.randint(0, 2)
    your_hand = (witch_hand + 1) % 3

    witch_hands.append(witch_hand)
    your_hands.append(your_hand)

print(f"{witch_hands[:10] = }")
print(f"{your_hands[:10]  = }")

output

witch_hands[:10] = [2, 1, 1, 2, 1, 0, 1, 2, 0, 2]
your_hands[:10]  = [0, 2, 2, 0, 2, 1, 2, 0, 1, 0]

To understand more about how the rock-paper-scissors plays are generated, we can read the CPython random.py source code. The call stack looks like:

The script uses Random.randint(0, 2)
… which calls Random.randrange(0, 3)
… which calls Random._randbelow(3)
… which points to Random._randbelow_with_getrandbits(3)
… which calls Random.getrandbits(2)
… which calls into C implementation _random_Random_getrandbits_impl()

Random.getrandbits(2) generates a 32 bit output from the PRNG and only returns the highest 2 bits, while Random._randbelow_with_getrandbits(3) will keep generating until Random.getrandbits(2) returns something strictly less than 3. To produce the winning your_random hands, we want to find a seed that will generate the right values in the highest 2 bits of each PRNG output.

Since we know our desired PRNG outputs, a symbolic Mersenne Twister cracker can be used to obtain a valid PRNG state that produces these outputs. Modifications to this reference implementation were made to recover the PRNG state immediately after seeding instead of the state after the outputs are generated.

Solve for PRNG statepython
# !wget https://raw.githubusercontent.com/icemonster/symbolic_mersenne_cracker/main/main.py -O untwister.py
from untwister import Untwister as _Untwister
import logging
logging.disable()

# Superclass Untwister to obtain PRNG state after seeding
# instead of PRNG state after outputs generated
class Untwister(_Untwister):
    def __init__(self):
        super().__init__()
        self.first_MT = self.MT

        # https://github.com/python/cpython/blob/main/Modules/_randommodule.c#L201
        # Index is 624 after seeding
        self.index = 624

    def get_random(self):
        # https://github.com/python/cpython/blob/main/Modules/_randommodule.c#L232
        # First MT state is set to 0x80000000 after seeding
        self.solver.add(self.first_MT[0] == 0x80000000)

        print(self.solver.check())
        model = self.solver.model()
        state = [
            model[x].as_long() if model[x] is not None else 0
            for x in self.first_MT
        ]

        result_state = (3, tuple(state+[624]), None)
        rand = random.Random()
        rand.setstate(result_state)
        return rand

ut = Untwister()
for your_hand in your_hands:
    res = bin(your_hand)[2:].zfill(2) + "?" * 30
    ut.submit(res)
ut_rand = ut.get_random()
ut_rand_state = ut_rand.getstate()[1][:-1]

# sanity check
for your_hand in your_hands:
    assert your_hand == ut_rand.randint(0, 2)

output

sat

Though we have a valid PRNG state that can generate winning outputs, we need to send the server a seed value that will create this state. We can study how PRNG seeding works again with some source code review:

The script uses Random.seed(seed)
… which calls into C implementation random_seed(seed)
… which calls init_by_array(seed)
… which does a bunch of math

For seeds that are python long arbitrary precision integers, the C function init_by_array(init_key) accepts the long represented as an array of 32-bit unsigned integers init_key with the least significant 32-bit integer coming first, then loops through them with some XORs and multiplications to create the initial PRNG state. We can re-implement init_by_array(init_key) in python and use z3 to solve for a valid init_key that is 624 32-bit unsigned integers long and produces the desired PRNG state. Finally we can submit this seed to the challenge server to get flag.

Solve for PRNG seedpython
from z3 import *

prng_N = 624

def u32(x):
    return x & 0xffffffff

# Note that LShR is used instead of ">>" operator
# unsigned 32 bit integers use logical bitshift, not arithmetic bitshift.

# https://github.com/python/cpython/blob/main/Modules/_randommodule.c#L186
def init_genrand(s):
    mt = [0 for _ in range(prng_N)]

    mt[0] = BitVecVal(s, 32)
    mti = 1
    while mti < prng_N:
        mt[mti] = u32(
            1812433253 * (mt[mti-1] ^ LShR(mt[mti-1], 30)) + mti
            # 1812433253 * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti
        )
        mti += 1
    return mt, mti

# https://github.com/python/cpython/blob/main/Modules/_randommodule.c#L209
def init_by_array(init_key):
    key_length = len(init_key)
    mt, mti = init_genrand(19650218)

    i, j = 1, 0
    k = prng_N if prng_N > key_length else key_length
    while k:
        mt[i] = u32(
            (mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1664525)) + init_key[j] + j
        )
        i, j = i + 1, j + 1
        if i >= prng_N:
            mt[0] = mt[prng_N-1]
            i = 1
        if j >= key_length:
            j = 0
        k -= 1

    k = prng_N - 1
    while k:
        mt[i] = u32(
            (mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1566083941)) - i
        )
        i += 1
        if i >= prng_N:
            mt[0] = mt[prng_N-1]
            i = 1
        k -= 1

    mt[0] = 0x80000000;

    return mt

seed_vars = [
    BitVec(f"seed_{i}", 32) for i in range(624)
]
seed_rand_state = init_by_array(seed_vars)

s = Solver()
for a, b in zip(seed_rand_state, ut_rand_state):
    s.add(a == b)
print(s.check())

model = s.model()
seed_init_key = [
    model[x].as_long() if model[x] is not None else 0
    for x in seed_vars
]
print(f"{seed_init_key[:10] = }")

output

sat
seed_init_key[:10] = [2785066542, 4109823319, 1943818831, 195508595, 4046365112, 359652855, 2071527069, 3612262978, 2265693527, 3400945710]

Convert seed and claim flagpython
seed_rand_seed = sum([x * (2 ** (idx * 32))for idx, x in enumerate(seed_init_key)])
print("seed_rand_seed =", str(seed_rand_seed)[:50], "...")

seed_rand = random.Random()
seed_rand.seed(seed_rand_seed)

# sanity check
assert seed_rand.getstate()[1][:-1] == ut_rand_state
for your_hand in your_hands:
    assert your_hand == seed_rand.randint(0, 2)

r.sendline(f"{hex(seed_rand_seed)[2:]}".encode())
print(r.recvall().decode())

output

seed_rand_seed = 47391526757246540556852465962283917972958287802376 ...
 What about your spell?
your spell: kurenaif: Amazing! Your spell is very powerful!!
kurenaif: OK. The flag is here. SECCON{https://youtu.be/h0GSFxoRhrc}

witches_symmetric_exam

By kurenaif

crypto witch made a exam. The exam has to communicate with witch and saying secret spell correctly. Have fun ;)

nc witches-symmetric-exam.seccon.games 8080

Attachments: problem.py

22 solves, 197 points

Challenge problem.pypython
from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
from Crypto.Util.Padding import pad, unpad
from flag import flag, secret_spell

key = get_random_bytes(16)
nonce = get_random_bytes(16)


def encrypt():
    data = secret_spell
    gcm_cipher = AES.new(key, AES.MODE_GCM, nonce=nonce)
    gcm_ciphertext, gcm_tag = gcm_cipher.encrypt_and_digest(data)

    ofb_input = pad(gcm_tag + gcm_cipher.nonce + gcm_ciphertext, 16)

    ofb_iv = get_random_bytes(16)
    ofb_cipher = AES.new(key, AES.MODE_OFB, iv=ofb_iv)
    ciphertext = ofb_cipher.encrypt(ofb_input)
    return ofb_iv + ciphertext

def decrypt(data):
    ofb_iv = data[:16]
    ofb_ciphertext = data[16:]
    ofb_cipher = AES.new(key, AES.MODE_OFB, iv=ofb_iv)

    try:
        m = ofb_cipher.decrypt(ofb_ciphertext)
        temp = unpad(m, 16)
    except:
        return b"ofb error"

    try:
        gcm_tag = temp[:16]
        gcm_nonce = temp[16:32]
        gcm_ciphertext = temp[32:]
        gcm_cipher = AES.new(key, AES.MODE_GCM, nonce=gcm_nonce)

        plaintext = gcm_cipher.decrypt_and_verify(gcm_ciphertext, gcm_tag)
    except:
        return b"gcm error"

    if b"give me key" == plaintext:
        your_spell = input("ok, please say secret spell:").encode()
        if your_spell == secret_spell:
            return flag
        else:
            return b"Try Harder"

    return b"ok"

print(f"ciphertext: {encrypt().hex()}")
while True:
    c = input("ciphertext: ")
    print(decrypt(bytes.fromhex(c)))

The server uses two AES-OFB and AES-GCM ciphers in series with the same key to encrypt some secret text and users can query decryption on some data. Different output is returned if padding errors or GCM tag verification errors are found, which points towards an AES padding oracle.

Get parameterspython
from pwn import *

context.log_level = "error"

r = remote("witches-symmetric-exam.seccon.games", 8080)
r.recvuntil(b"ciphertext: ")
enc = bytes.fromhex(r.recvline().decode())
print(f"{len(enc)  = }")
print(f"{enc.hex() = }")

output

len(enc)  = 80
enc.hex() = 'eba5836c9b1b7892a39cd7031fd5d89d0f8b66e0e00447aec9d9ffcceaa11b6a3b95fc35580fc578b90b186a8948391beca9c91e538a8d4d3d53eb3dd8404c27f2b8eafa5add251eb1bfd41a32aa38fd'

AES-OFB decrypts one block of ciphertext ct with initiation vector iv by doing pt = unpad(enc<key>(iv) ^ ct) and prouduces different results if unpad succeeds or fails. This is effectively an AES-ECB encryption oracle as we can adjust the tail bytes of ct until unpad succeeds, thus finding enc<key>(iv) = expected_padding ^ ct.

Decryption oracle routinespython
def bxor(*args):
    if len(args) == 1:
        return args[0]
    a, b = args[0], args[1:]
    return bytes([i ^ j for i, j in zip(a, bxor(*b))])

def query(xs):
    r.sendline("\n".join([x.hex() for x in xs]).encode())
    ress = []
    for _ in xs:
        r.recvuntil(b"ciphertext: ")
        res = r.recv(5).strip().decode()
        if "b'ofb" in res:
            ress.append("pad")
        elif "b'gcm" in res:
            ress.append("gcm")
        elif "o', p" in res:
            ress.append("spell")
        elif "b'ok'" in res:
            ress.append("ok")
        else:
            raise ValueError(res)
    return ress

def leak_enc(pln):
    enc = [0 for _ in range(16)]

    for pos in range(16):
        print(".", end="", flush=True)
        expected_padding = ([0] * 16 + [pos+1] * (pos+1))[-16:]

        found = []
        probe = [0] * 16

        xs = []
        for i in range(256):
            probe[15-pos] = i
            try_block_ofb = pln + bxor(enc, expected_padding, probe)
            xs.append(try_block_ofb)
        ress = query(xs)
        for i, res in enumerate(ress):
            if res == "gcm":
                found.append(i)
        if len(found) != 1:
            raise ValueError("???", pos, found)

        enc[15-pos] = found[0]
    print()

    return bytes(enc)

To decrypt the OFB phase, leak enc<key>(iv), then enc<key>(enc<key>(iv)) and so on to get the whole AES-OFB cipher stream that the plaintext is XOR-ed with. We can verify that the decryption is correct by checking for valid padding on gcm_enc.

Decrypt OFBpython
from Crypto.Util.Padding import unpad

ofb_iv = enc[:16]
ofb_enc = enc[16:]

print(f"{ofb_iv.hex()     = }")

ofb_stream = ofb_iv
for block in range(4):
    ofb_stream += leak_enc(ofb_stream[-16:])
ofb_stream = ofb_stream[16:]

print(f"{ofb_stream.hex() = }")

ofb_dec = bxor(ofb_enc, ofb_stream)
gcm_tag, gcm_nonce, gcm_enc = ofb_dec[:16], ofb_dec[16:32], unpad(ofb_dec[32:], 16)

print(f"{gcm_tag.hex()    = }")
print(f"{gcm_nonce.hex()  = }")
print(f"{gcm_enc.hex()    = }")

output

ofb_iv.hex()     = 'eba5836c9b1b7892a39cd7031fd5d89d'
................
................
................
................
ofb_stream.hex() = '23fdad43a2f057a7d2b7796e90bc05c2e60823306dfb1f139117cc63738a05f2c6e2511b07e4ed91f2841066f453217886601ef80387309bb9b7dc123aa230f5'
gcm_tag.hex()    = '2c76cba342f410091b6e86a27a1d1ea8'
gcm_nonce.hex()  = 'dd9ddf0535f4da6b281cd409fac23ce9'
gcm_enc.hex()    = '2a4b9805546e60dccfd7fb5b2c136d5f74d8f402595a1585'

It turns out that this encryption oracle is also sufficient to break AES-GCM encryption and decryption because internally these operations only require AES-ECB encryption!

We can derive the parameters h0 and j0 of the AES-GCM cipher using the encryption oracle. These parameters are used to calculate the nonce for the internal AES-CTR cipher stream and are also used for the AES-GCM tag generation. Referring to pycryptodome source helped a lot for this step.

GCM parameterspython
from Crypto.Util.number import long_to_bytes, bytes_to_long
from Crypto.Cipher._mode_gcm import _GHASH as GHASH, _ghash_clmul as ghash_c

# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L223-L226
h0 = leak_enc(b"\x00" * 16)
print(f"{h0.hex() = }")

# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L232-L236
nonce = gcm_nonce
fill = (16 - (len(nonce) % 16)) % 16 + 8
ghash_in = (nonce + b'\x00' * fill + long_to_bytes(8 * len(nonce), 8))
j0 = GHASH(h0, ghash_c).update(ghash_in).digest()
print(f"{j0.hex() = }")

output

................
h0.hex() = 'dee52a0c81a9ed9e2645c2453ea2131b'
j0.hex() = '991ef958aa7192caa6b5b2f7754743f5'

We can obtain the internal AES-CTR cipher stream by simulating the counter increment and leaking enc<key>(j0+1) and enc<key>(j0+2). We can then decrypt the secret_spell string by XOR-ing with this cipher stream.

Decrypt GCMpython
# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L239-L245
# nonce_ctr = j0[:12]
# iv_ctr = (bytes_to_long(j0) + 1) & 0xFFFFFFFF
# nonce_iv_bytes = nonce_ctr + bytes.fromhex(hex(iv_ctr)[2:].zfill(8))
block_one_ctr = bytes.fromhex(hex(int(j0.hex(), 16) + 1)[2:])
block_two_ctr = bytes.fromhex(hex(int(j0.hex(), 16) + 2)[2:])

gcm_stream = leak_enc(block_one_ctr) + leak_enc(block_two_ctr)
gcm_pln = bxor(gcm_stream, gcm_enc)
secret_spell = gcm_pln
print(f"{secret_spell = }")

output

................
................
secret_spell = b'decrypt_all!!277260221!!'

Finally to claim the flag we need to encrypt and sign the message "give me key". We can reuse the previous nonces and IVs which means the cipher streams stay the same, so encryption will just involve XOR-ing the message with streams in the right order. A valid tag can be generated by processing the GHASH locally and XOR-ing with enc<key>(j0). This lets us claim the flag.

Claim flagpython
from Crypto.Util.Padding import pad

signer = GHASH(h0, ghash_c)
token_dec = b"give me key"

# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L372-L379
# > encrypt and digest > encrypt
token_enc = bxor(token_dec, gcm_stream)
msg_len = len(token_enc)
# signer.update(token_enc) # defer to later for block alignment

# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L459-L462
# > encrypt and digest > digest
signer.update(token_enc + b"\x00" * (16 - msg_len))
signer.update(long_to_bytes(8 * 0, 8) + long_to_bytes(8 * msg_len, 8))
tag_dec = signer.digest()

# https://github.com/Legrandin/pycryptodome/blob/master/lib/Crypto/Cipher/_mode_gcm.py#L465
# > encrypt and digest > digest > self._tag_cipher.encrypt
j0_stream = leak_enc(j0)
tag_enc = bxor(tag_dec, j0_stream)

print(f"{tag_enc.hex() = }")

payload = ofb_iv + bxor(pad(tag_enc + gcm_nonce + token_enc, 16), ofb_stream)
print(f"{payload.hex() = }")

r.sendline(payload.hex().encode())
r.sendline(secret_spell)
flag = r.recvuntil(b"}").decode().strip()
print(flag)

output

................
tag_enc.hex() = '76c2626da50248e3cc8dea847f7dc442'
payload.hex() = 'eba5836c9b1b7892a39cd7031fd5d89d553fcf2e07f21f441e3a93eaefc1c1803b95fc35580fc578b90b186a8948391befa5dc090a979c32375afe63f156247d'
error'
ciphertext: ok, please say secret spell:b'SECCON{you_solved_this!?I_g1ve_y0u_symmetr1c_cipher_mage_certificate}

insufficient

By Xornet

SUGOI SECRET SHARING SCHEME with insufficient shares

Attachments: dist.tar.gz

33 solves, 164 points

Challenge problem.pypython
from random import randint
from Crypto.Util.number import getPrime, bytes_to_long
from secret import FLAG


# f(x,y,z) = a1*x + a2*x^2 + a3*x^3
#          + b1*y + b2*y^2 + b3*y^3
#          + c*z + s mod p
def calc_f(coeffs, x, y, z, p):
    ret = 0
    ret += x * coeffs[0] + pow(x, 2, p) * coeffs[1] + pow(x, 3, p)*coeffs[2]
    ret += y * coeffs[3] + pow(y, 2, p) * coeffs[4] + pow(y, 3, p)*coeffs[5]
    ret += z * coeffs[6]
    ret += coeffs[7]

    return ret % p

p = getPrime(512)

# [a1, a2, a3, b1, b2, b3, c, s]
coeffs = [randint(0, 2**128) for _ in range(8)]

key = 0
for coeff in coeffs:
    key <<= 128
    key ^= coeff

cipher_text = bytes_to_long(FLAG) ^ key
print(cipher_text)

shares = []
for _ in range(4):
    x = randint(0, p)
    y = randint(0, p)
    z = randint(0, 2**128)

    w = calc_f(coeffs, x, y, z, p)
    packed_share = ((x,y), w)
    shares.append(packed_share)

print(p)
print(shares)

128-bit coeffs $a_1$ to $a_3$ / $b_1$ to $b_3$ / $c$ / $s$ are generated on the server and are kept secret and are needed to recover the flag. A 512-bit prime $p$ is published and 4 shares are calculated where $x, y < p$ and $z < 2^{128}$ . We are given $x$ , $y$ and the result of calc_f $w$ for each share.

python

# challenge problem.py

# f(x,y,z) = a1*x + a2*x^2 + a3*x^3
#          + b1*y + b2*y^2 + b3*y^3
#          + c*z + s mod p
def calc_f(coeffs, x, y, z, p):
    ret = 0
    ret += x * coeffs[0] + pow(x, 2, p) * coeffs[1] + pow(x, 3, p)*coeffs[2]
    ret += y * coeffs[3] + pow(y, 2, p) * coeffs[4] + pow(y, 3, p)*coeffs[5]
    ret += z * coeffs[6]
    ret += coeffs[7]

    return ret % p

Expand parameterspython
ct = 115139400156559163067983730101733651044517302092738415230761576068368627143021367186957088381449359016008152481518188727055259259438853550911696408473202582626669824350180493062986420292176306828782792330214492239993109523633165689080824380627230327245751549253757852668981573771168683865251547238022125676591
p = 8200291410122039687250292442109878676753589397818032770561720051299309477271228768886216860911120846659270343793701939593802424969673253182414886645533851
shares = [
    ((6086926015098867242735222866983726204461220951103360009696454681019399690511733951569533187634005519163004817081362909518890288475814570715924211956186561, 180544606207615749673679003486920396349643373592065733048594170223181990080540522443341611038923128944258091068067227964575144365802736335177084131200721), 358596622670209028757821020375422468786000283337112662091012759053764980353656144756495576189654506534688021724133853284750462313294554223173599545023200),
    ((1386358358863317578119640490115732907593775890728347365516358215967843845703994105707232051642221482563536659365469364255206757315665759154598917141827974, 4056544903690651970564657683645824587566358589111269611317182863269566520886711060942678307985575546879523617067909465838713131842847785502375410189119098), 7987498083862441578197078091675653094495875014017487290616050579537158854070043336559221536943501617079375762641137734054184462590583526782938983347248670),
    ((656537687734778409273502324331707970697362050871244803755641285452940994603617400730910858122669191686993796208644537023001462145198921682454359699163851, 7168506530157948082373212337047037955782714850395068869680326068416218527056283262697351993204957096383236610668826321537260018440150283660410281255549702), 1047085825033120721880384312942308021912742666478829834943737959325181775143075576517355925753610902886229818331095595005460339857743811544053574078662507),
    ((5258797924027715460925283932681628978641108698338452367217155856384763787158334845391544834908979711067046042420593321638221507208614929195171831766268954, 4425317882205634741873988391516678208287005927456949928854593454650522868601946818897817646576217811686765487183061848994765729348913592238613989095356071), 866086803634294445156445022661535120113351818468169243952864826652249446764789342099913962106165135623940932785868082548653702309009757035399759882130676)
]

F = Zmod(p)

share_xxxyyy = [
    [ ZZ(i) for i in [F(x), F(x) ^ 2, F(x) ^ 3, F(y), F(y) ^ 2, F(y) ^ 3]]
    for (x, y), _ in shares
]
share_w = [w for _, w in shares]

Since we know $x$ and $y$ , we can calculate the corresponding $x^2$ / $x^3$ / $y^2$ / $y^3$ values and try to model this as a closest vector problem:

\mathbf{B} = \begin{bmatrix} x_0 & \cdots & x_3 & 2^{128} & \\ \vdots & \ddots & \vdots & & \ddots \\ y^3_0 & \cdots & y^3_3 & & & 2^{128} \\ p & & \\ & \ddots & \\ & & p \\ \end{bmatrix} \\[8pt] \textbf{x} = \begin{pmatrix} a_1 & \cdots & b_3 & - \lfloor \frac{w_0}{p} \rfloor & \cdots & - \lfloor \frac{w_3}{p} \rfloor \\ \end{pmatrix} \\[4pt] \textbf{u} = \begin{pmatrix} w_0 - cz_0 - s & \cdots & w_3 - cz_3 - s & 2^{128} a_1 & \cdots & 2^{128} b_3 \\ \end{pmatrix} \\[4pt] \textbf{t} = \begin{pmatrix} w_0 & \cdots & w_3 & 2^{255} & \cdots & 2^{255} \\ \end{pmatrix} \\[4pt] \mathbf{x} \mathbf{B} = \textbf{u} \approx \textbf{t}

A factor of $2^{128}$ is added to the part of the lattice generating $a_1$ to $b_3$ to make their residuals in the same order of magnitude as the expected 256-bit residuals of $cz+s$ .

For a closest vector $\textbf{u}$ generated by $\mathbf{B}$ to reference vector $\textbf{t}$ , $\textbf{u}$ differs from $\textbf{t}$ in $w_0$ to $w_3$ by its $cz+s$ term, while the later terms will be near to $2^{128} a_1$ to $2^{128} b_3$ . $c$ and $s$ can then be recovered by taking the GCD of differences between residues, obtaining all the data required to recover the flag.

Solve CVPpython
# https://jgeralnik.github.io/writeups/2021/08/12/Lattices/
def closest_vector(B, target):
    # Babai's Nearest Plane algorithm
    M = B.LLL()
    G = M.gram_schmidt()[0]
    small = target
    for _ in range(1):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -= M[i] * c
    return target - small

r, c = 11, 11

two_127 = 2 ^ 127
two_128 = 2 ^ 128
large = 2 ^ 1024

mat = [
    [0 for _ in range(c)]
    for _ in range(r)
]
vec = [ 0 for _ in range(c) ]

for coeff_i in range(6):
    for share_i in range(4):
        mat[coeff_i][share_i] = share_xxxyyy[share_i][coeff_i]
    mat[coeff_i][4 + coeff_i] = two_128
    vec[coeff_i] = two_127 * two_128

for share_i in range(4):
    mat[6 + share_i][share_i] = p
    mat[10][share_i] = - shares[share_i][1]

mat[10][10] = large
vec[10] = large

mat = Matrix(ZZ, mat)
vec = vector(vec)

cv = closest_vector(mat, vec)
assert cv[10] == large

for idx, cvi in enumerate(cv):
    print(f"cv[{idx}] = {cvi}")

output

cv[0] = -73127182509659574936304130186390232855613411712618127387302114362808513444038
cv[1] = -21323554641234012731873431347941675841849210679985598800027345190229736374864
cv[2] = -95332596761823814479686618419564498660798012792472282519243854651578178909353
cv[3] = -65202559187559307765157064732030011588113460469631415668829640873318085305823
cv[4] = 108872274582080884429104542718114951764799087578511053878950064648738360524800
cv[5] = 51808446279407138673963965459500483574659336067433398358542736292199876526080
cv[6] = 46874495483872404296318603859111203660545082957551217054277798423995804024832
cv[7] = 114770789402085722865307263932237123446182777168313585667126867879815270105088
cv[8] = 51217024666795342916098068957979173083931580539085821138892284370538977034240
cv[9] = 9527304801756674193386489592332566492258743922045146824371698689838183088128
cv[10] = 179769313486231590772930519078902473361797[...]10684586298239947245938479716304835356329624224137216

Calculate coeffspython
coeffs_6 = [
    i // two_128
    for i in cv[4:10]
]

czs = [
    (w - sum([a * b for a, b in zip(xxxyyyy, coeffs_6)])) % p
    for xxxyyyy, w in zip(share_xxxyyy, share_w)
]
c6 = gcd(czs[1] - czs[0], czs[2] - czs[0])
c7 = czs[0] % c6

coeffs = [*coeffs_6, c6, c7]
for idx, coeff_i in enumerate(coeffs):
    print(f"coeffs[{idx}] = {coeff_i}")

output

coeffs[0] = 319946859331022505606006682830489529550
coeffs[1] = 152251339815807627609342474617581741055
coeffs[2] = 137751761597342098624908697775689190697
coeffs[3] = 337281036453915579622200616302875159873
coeffs[4] = 150513307904359194457545638585602396040
coeffs[5] = 27998232432567560780529247469815955088
coeffs[6] = 285109170934241472003856820431690507519
coeffs[7] = 86246982746739283466217140132251503442

Claim flagpython
key = 0
for coeff in coeffs:
    key <<= 128
    key = key ^^ coeff
flag = ct ^^ key

bytes.fromhex(hex(flag)[2:])

output

b'SECCON{Unfortunately_I_could_not_come_up_with_a_more_difficult_problem_than_last_year_sorry...-6fc18307d3ed2e7673a249abc2e0e22c}'

this_is_not_lsb

By kurenaif

Tired of difficult problems? Ok, I give you a simple LSB Padding Oracle problem. Ah, my magic has exploded… Sorry

nc this-is-not-lsb.seccon.games 8080

Attachments: problem.py

34 solves, 162 points

Challenge problem.pypython
from Crypto.Util.number import *
from flag import flag

p = getStrongPrime(512)
q = getStrongPrime(512)
e = 65537
n = p * q
phi = (p - 1) * (q - 1)

d = pow(e, -1, phi)

print(f"n = {n}")
print(f"e = {e}")
print(f"flag_length = {flag.bit_length()}")

# Oops! encrypt without padding!
c = pow(flag, e, n)
print(f"c = {c}")

# padding format: 0b0011111111........
def check_padding(c):
    padding_pos = n.bit_length() - 2
    m = pow(c, d, n)

    return (m >> (padding_pos - 8)) == 0xFF

while True:
    c = int(input("c = "))
    print(check_padding(c))

The server gives us a RSA public key parameters and the encryption c of flag without padding, and a decryption oracle which reveals if the decryption is between 0b0011111111000... and 0b0011111111111...; let us call this $\text{dec}_L$ and $\text{dec}_U$ . Because of RSA homomorpism where multiplication of ciphertexts is equivalent to multiplication plaintexts, we can make queries in the form $c \cdot k^e \bmod n$ which will decrypt to $\text{flag} \cdot k \bmod n$ and tells us if this decryption result is in the oracle’s interval.

From the the SECCON{... flag format and the server output revealing that the flag is 439 bits long, we can assume these are the top bytes of the flag and pad the rest to narrow down the interval of possible flag values; let us call these bounds $\text{flag}_L$ and $\text{flag}_U$ .

We then binary search on the possible values of $\text{flag}$ by calculating a mid-point $\text{flag}_M = \frac{\text{flag}_L + \text{flag}_U}{2}$ and querying the decryption of $c \cdot \lfloor \frac{\text{dec}_L}{\text{flag}_M} \rfloor ^e$ . This will decrypt to $\text{flag} \cdot \lfloor \frac{\text{dec}_L}{\text{flag}_M} \rfloor$ ¹ and from the oracle output we can gain useful information about the value of $\text{flag}$ :²

When the oracle returns True, $\text{flag} \cdot \lfloor \frac{\text{dec}_L}{\text{flag}_M} \rfloor > \text{dec}_L$ and therefore $\text{flag} > \text{flag}_M$
When the oracle returns False, $\text{flag} \cdot \lfloor \frac{\text{dec}_L}{\text{flag}_M} \rfloor < \text{dec}_L$ and therefore $\text{flag} < \text{flag}_M$

This also requires $\text{flag} \cdot \lfloor \frac{\text{dec}_L}{\text{flag}_M} \rfloor < \text{dec}_U$ but using known flag prefix this will always be true. A linear search for a good starting $\text{flag}_M$ can be done if we don’t have known flag prefix.

With this information, we can narrow down the range of possible $\text{flag}$ after each query, essentially binary searching for the flag.

Exploit codepython
from pwn import *

context.log_level = "error"

# ====== Get parameters ======

r = remote("this-is-not-lsb.seccon.games", 8080)
r.recvuntil(b"n = ")
n = int(r.recvline().strip().decode())
r.recvuntil(b"e = ")
e = int(r.recvline().strip().decode())
r.recvuntil(b"flag_length = ")
flag_length = int(r.recvline().strip().decode())
r.recvuntil(b"c = ")
c = int(r.recvline().strip().decode())

print(f"{n           = }")
print(f"{e           = }")
print(f"{flag_length = }")
print(f"{c           = }")

def query(k):
    y = (pow(k, e, n) * c) % n
    r.recvuntil(b"c = ")
    r.sendline(f"{y}".encode())
    res = r.recvline().decode().strip()
    if res == "True":
        return True
    elif res == "False":
        return False
    else:
        raise ValueError(res)

dec_lb = int("0011111111".ljust(n.bit_length(), "0"), 2)
dec_ub = int("0011111111".ljust(n.bit_length(), "1"), 2)
flag_lb = int((b"SECCON{"+ b"\x00" * 48).hex(), 16)
flag_ub = int((b"SECCON{"+ b"\xff" * 48).hex(), 16)

# ====== Binary search ======

while flag_ub - flag_lb > 10:
    flag_md = (flag_lb + flag_ub) // 2
    coef = dec_lb // flag_md
    if query(coef):
        print("-", end="", flush=True)
        flag_lb = flag_md
    else:
        print("+", end="", flush=True)
        flag_ub = flag_md
print()
flag = bytes.fromhex(hex(flag_lb)[2:])
print(f"{flag = }")

output

n           = 13843646552185108127[...]578679382305964423040143
e           = 65537
flag_length = 439
c           = 83362066469299840911[...]29224401955722779580980
+-+-+---+--++-+-+-++--+++-++++--++[...]-++--+++--++-+-++-++++-+----
flag = b'SECCON{WeLC0me_t0_tHe_MirRoR_LaNd!_tHIs_is_lSb_orAcLe!w'

Alternative solution with Inequality-CVP

Consider what happens if several $k$ are randomly generated and $c \cdot k^e \bmod n$ is queried until the oracle returns True. This means that we have some found $k_i$ where $\text{dec}_L < \text{flag} \cdot k_i \bmod n < \text{dec}_U$ , where after some rearranging we have $\text{dec}_L < \text{flag} \cdot k_i - a_i \cdot n < \text{dec}_U$ . With enough random $k_i$ , we can model this as a closest vector problem for solving inequalities.

\mathbf{B} = \begin{bmatrix} k_0 & \cdots & k_{49} & z \\ n \\ & \ddots \\ & & n \\ \end{bmatrix} \\[8pt] \textbf{x} = \begin{pmatrix} \text{flag} & -a_0 & \cdots & -a_{49} \\ \end{pmatrix} \\[4pt] \textbf{u} = \begin{pmatrix} \text{flag} \cdot k_0 - a_0 \cdot n & \cdots & \text{flag} \cdot k_{49} - a_{49} \cdot n & z \cdot \text{flag} \\ \end{pmatrix} \\[4pt] \textbf{t} = \begin{pmatrix} \frac{\text{dec}_L + \text{dec}_U}{2} & \cdots & \frac{\text{dec}_L + \text{dec}_U}{2} & z \cdot \frac{\text{flag}_L + \text{flag}_U}{2} \\ \end{pmatrix} \\[4pt] \mathbf{x} \mathbf{B} = \textbf{u} \approx \textbf{t}

We might not know the exact value of $c \cdot k \bmod n$ , but guessing that they are around $\frac{\text{dec}_L + \text{dec}_U}{2}$ is sufficient to help solve for $\text{flag}$ . We also introduce a scaling term $z = \lfloor \frac{\text{dec}_U - \text{dec}_L}{\text{flag}_U - \text{flag}_L} \rfloor$ which will ensure the residues of the $| z \cdot \text{flag} - z \cdot \frac{\text{flag}_L + \text{flag}_U}{2} |$ term will be in the same magnitude as the resides from other terms. For more information about this trick, take a look at rkm0959’s work on inequality CVP.

Since 10 bytes are fixed by the padding oracle, a random $k$ has a $1$ in $2^{10}$ chance of its decryption falling in the appropriate range for the oracle to return True, which means to obtain $50$ valid $k$ we can expect it to take $50 \cdot 2^{10} = 51 \, 200$ queries which can be done within the time limit.

Exploit codesage
from pwn import *

# https://jgeralnik.github.io/writeups/2021/08/12/Lattices/
def closest_vector(B, target):
    # Babai's Nearest Plane algorithm
    M = B.LLL()
    G = M.gram_schmidt()[0]
    small = target
    for _ in range(1):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -= M[i] * c
    return target - small

context.log_level = "error"

# ====== Get parameters ======

r = remote("this-is-not-lsb.seccon.games", 8080)
r.recvuntil(b"n = ")
n = int(r.recvline().strip().decode())
r.recvuntil(b"e = ")
e = int(r.recvline().strip().decode())
r.recvuntil(b"flag_length = ")
flag_length = int(r.recvline().strip().decode())
r.recvuntil(b"c = ")
c = int(r.recvline().strip().decode())

print(f"{n           = }")
print(f"{e           = }")
print(f"{flag_length = }")
print(f"{c           = }")

def query_many(ks):
    reqs = [
        (c * pow(k, e, n)) % n
        for k in ks
    ]
    req = "\n".join([
        str(i)
        for i in reqs
    ])
    r.sendline(req.encode())
    ress = [
        [r.recvuntil(b"c = "), r.recvline().decode()[0] == "T"][1]
        for _ in ks
    ]
    return ress

dec_lb = int("0011111111".ljust(n.bit_length(), "0"), 2)
dec_ub = int("0011111111".ljust(n.bit_length(), "1"), 2)
flag_lb = int((b"SECCON{"+ b"\x00" * 48).hex(), 16)
flag_ub = int((b"SECCON{"+ b"\xff" * 48).hex(), 16)

# ====== Farm for valid k ======

n_samples = 50
samples = []
while len(samples) < n_samples:
    ks = [randint(2, n) for _ in range(512)]
    ress = query_many(ks)
    for k, res in zip(ks, ress):
        if res:
            samples.append(k)
            print(".", end="", flush=True)
print()
n_samples = len(samples)
print(f"{n_samples = }")

# ====== Inequality-CVP ======

rows, cols = n_samples + 1, n_samples + 1
mat = [
    [0 for _ in range(cols)]
    for _ in range(rows)
]

k_flag_midpoint = (dec_lb + dec_ub) // 2
k_flag_range = dec_ub - dec_lb

flag_midpoint = (flag_lb + flag_ub) // 2
flag_range = flag_ub - flag_lb

flag_scale = k_flag_range // flag_range

mat[0][-1] = flag_scale
for idx, s in enumerate(samples):
    mat[0][idx] = s
    mat[1+idx][idx] = n

vec = [k_flag_midpoint] * n_samples + [flag_midpoint * flag_scale]

mat = Matrix(ZZ, mat)
vec = vector(vec)

cv = closest_vector(mat, vec)
flag = cv[-1] // flag_scale
flag_bytes = bytes.fromhex(hex(flag)[2:])
print(f"{flag_bytes = }")

output

n           = 12274371278327362987[...]800083923786587181356777
e           = 65537
flag_length = 439
c           = 56926305483733870652[...]67041160004687782469777
............................................................
n_samples = 51
flag_bytes = b'SECCON{WeLC0me_t0_tHe_MirRoR_LaNd!_tHIs_is_lSb_orAcLe!}'

Also see SekaiCTF EZMaze and DUCTF rsa interval oracle which has similar themes on binary search / inequality solving.

BBB

By Xornet

Sometimes I can’t distinguish between “b” and “d”

nc BBB.seccon.games 8080

Attachments: dist.tar.gz

50 solves, 136 points

Challenge chall.pypython
from Crypto.Util.number import bytes_to_long, getPrime
from random import randint
from math import gcd
from secret import FLAG
from os import urandom

assert len(FLAG) < 100


def generate_key(rng, seed):
    e = rng(seed)
    while True:
        for _ in range(randint(10,100)):
            e = rng(e)
        p = getPrime(1024)
        q = getPrime(1024)
        phi = (p-1)*(q-1)
        if gcd(e, phi) == 1:
            break

    n = p*q
    return (n, e)

def generate_params():
    p = getPrime(1024)
    a = randint(0, p-1)

    return (p,a)

def main():
    p,a = generate_params()
    print("[+] The parameters of RNG:")
    print(f"{a=}")
    print(f"{p=}")
    b = int(input("[+] Inject [b]ackdoor!!: "))
    rng = lambda x: (x**2 + a*x + b) % p

    keys = []
    seeds = []
    for i in range(5):
        seed = int(input("[+] Please input seed: "))
        seed %= p
        if seed in seeds:
            print("[!] Same seeds are not allowed!!")
            exit()
        seeds.append(seed)
        n, e = generate_key(rng, seed)
        if e <= 10:
            print("[!] `e` is so small!!")
            exit()

        keys.append((n,e))

    flag = bytes_to_long(FLAG + urandom(16))
    for n,e in keys:
        c = pow(flag, e, n)
        print("[+] Public Key:")
        print(f"{n=}")
        print(f"{e=}")
        print("[+] Cipher Text:", c)

if __name__ == "__main__":
    main()

The server encrypts the flag with 5 RSA keypairs with e that is determined by the function $\text{rng}(x) = x^2 + ax + b \bmod p$ . The key generation procedure does seed = rng(seed) a random number of times and the end result is the e parameter for the RSA key.

The prime $p$ and random $a$ are generated by the server, but we have control over the parameter b and 5 initial values of seed.

Since the padded length of FLAG is at most 928 bits long, 5 pairs of 2048-bit RSA key and an e=11 is vulnerable to Hastad’s broadcast attack since $928 \cdot 11 = 10208 < 5 \cdot 2048 = 10240$ . The issue now is how to select b and 5 seed to get e=11 multiple times.

The first observation is that we want the function to be “stable” around seed=11; after reaching seed=11 any further operations of seed = rng(11) should not change seed. This implies that $\text{rng}(11) = 11 = (11)^2 + a \cdot 11 + b \bmod p$ , and with this we can solve for the value of $b$ .

We can now send the first seed as 11, but are there other values where $\text{rng}(\text{seed}) = 11$ ? This is a quadratic equation which can have 2 roots, of which one will be 11 and the other can be some large number. Since this equation is in a prime ring modulo $p$ , we can easily solve for this other root $s\prime$ where $\text{rng}(s\prime) = 11$ to get a second possible seed value. To generate more possible seeds, we can solve for more seeds $s\prime\prime$ where $\text{rng}(s\prime\prime) = s\prime$ and so on until we get enough seeds for 5 keypairs.

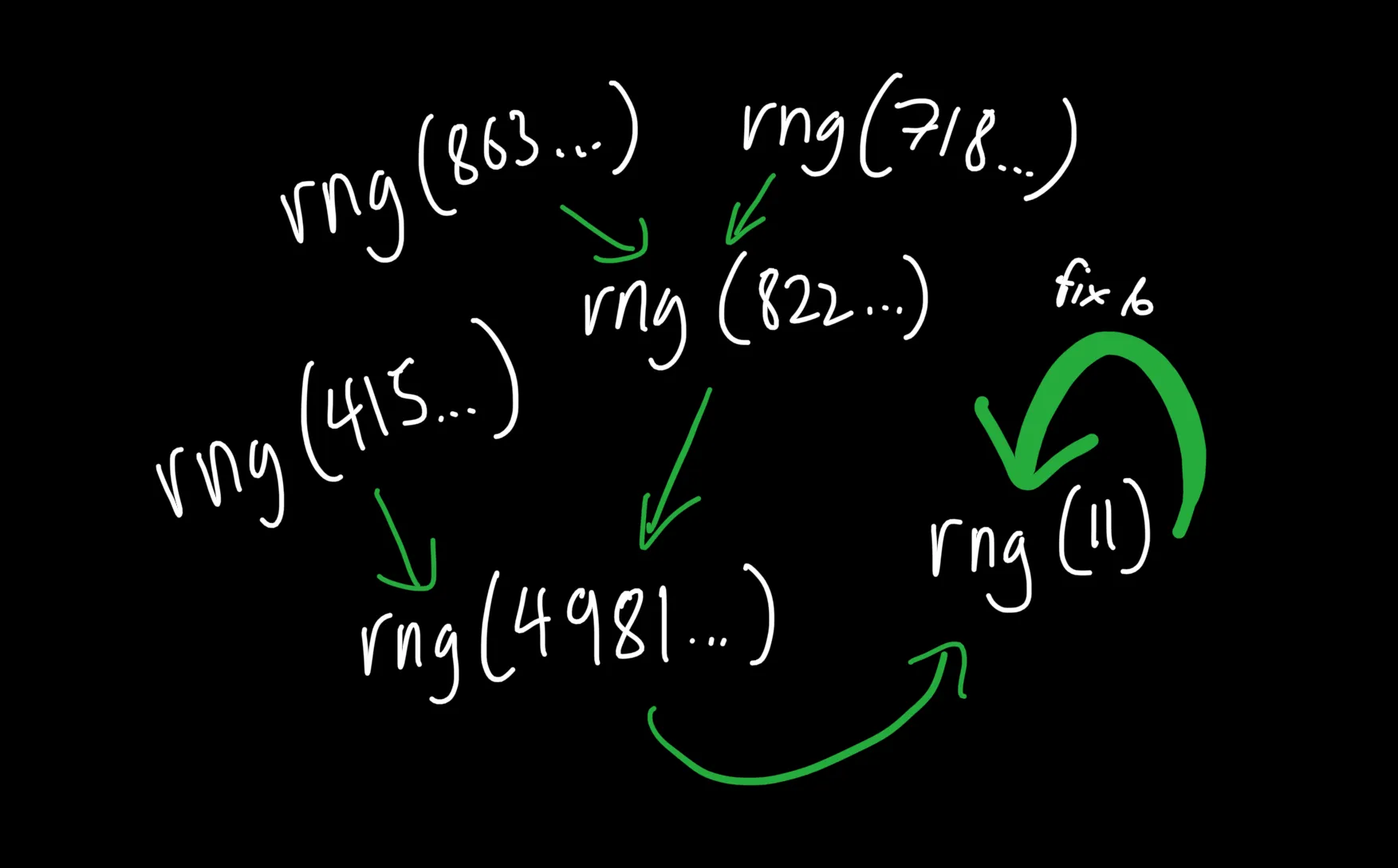
Finally, we can submit these 5 seeds and regenerate $\text{flag}^{11}$ over the integers using the Chinese Remainder Theorem, then get flag using integer roots.

Exploit codesage
# ====== Get parameters ======

from pwn import *

context.log_level = "error"

r = remote("BBB.seccon.games", 8080)
r.recvuntil(b"a=")
a = int(r.recvline().decode().strip())
r.recvuntil(b"p=")
p = int(r.recvline().decode().strip())

print(f"{a = }")
print(f"{p = }")

# ====== Calculate b ======

F = Zmod(p)
R.<x> = PolynomialRing(F, "x")

e = 11
eq = e ^ 2 + a * e + x - e
b = -eq.coefficients()[0]

print(f"{b = }")
print(f"{(x ^ 2 + a * x + b).subs(x=11) = }")

# ====== Find other roots ======

good_roots = [e]
search_roots = [e]

while search_roots and len(good_roots) < 5:
    root = search_roots.pop()
    eq = (x ^ 2 + a * x + b - root)
    for new_root, _ in eq.roots():
        if new_root in good_roots:
            continue
        print(f"rng({new_root}) = {root}")
        good_roots.append(new_root)
        search_roots.append(new_root)

print(f"{len(good_roots) = }")
assert len(good_roots) >= 5

# ====== Claim flag ======

r.recvuntil(b"[+] Inject [b]ackdoor!!: ")
r.sendline(f"{b}".encode())

for root in good_roots[:5]:
    r.recvuntil(b"[+] Please input seed: ")
    r.sendline(f"{root}".encode())

encs = []
for _ in good_roots[:5]:
    r.recvuntil(b"n=")
    n = int(r.recvline().decode().strip())
    r.recvuntil(b"e=")
    e = int(r.recvline().decode().strip())
    r.recvuntil(b"[+] Cipher Text: ")
    c = int(r.recvline().decode().strip())
    encs.append((n, e, c))

flag_e11 = CRT_list([i[2] for i in encs], [i[0] for i in encs])
flag_int = flag_e11.nth_root(11)
flag = bytes.fromhex(hex(int(flag_int))[2:])
print(f"{flag = }")

output

a = 58565556875033097418[...]43915055492039312594008
p = 10838179308804807042[...]624848130251995513098473
b = 60696329029243509419[...]6023171099540640056640
(x ** Integer(2) + a * x + b).subs(x=Integer(11)) = 11
rng(49816236213014973005[...]80933074759956200504454) = 11
rng(41590708505742891949[...]60452743016290828808379) = 49816236213014973005[...]80933074759956200504454
rng(82255277072720810564[...]0480331743665371696086) = 49816236213014973005[...]80933074759956200504454
rng(86352831126465586764[...]90103301110960958533298) = 82255277072720810564[...]0480331743665371696086
rng(71845198174597456665[...]15677903900990755069640) = 82255277072720810564[...]0480331743665371696086
len(good_roots) = 6
flag = b'SECCON{Can_you_find_d_in_bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbdbbbbbbbbbbbbbbbbbbbbbbbbbbbbb?}c\x1au\xc2Z\xec\xa0?>N=}\x1dj\xe1|'

pqpq

By kurenaif

Warm your hands first. It’s not obvious, right?

Attachments: output.txt problem.py

112 solves, 96 points

Challenge problem.pypython
from Crypto.Util.number import *
from Crypto.Random import *
from flag import flag

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
n = p * q * r
e = 2 * 65537

assert n.bit_length() // 8 - len(flag) > 0
padding = get_random_bytes(n.bit_length() // 8 - len(flag))
m = bytes_to_long(padding + flag)

assert m < n

c1p = pow(p, e, n)
c1q = pow(q, e, n)
cm = pow(m, e, n)
c1 = (c1p - c1q) % n
c2 = pow(p - q, e, n)

print(f"e = {e}")
print(f"n = {n}")
# p^e - q^e mod n
print(f"c1 = {c1}")
# (p-q)^e mod n
print(f"c2 = {c2}")
# m^e mod n
print(f"cm = {cm}")

This is a case of multi-prime RSA with abnormal exponent $e=65537 \cdot 2$ .

We can recover $p$ , $q$ and $r$ by manipulating leaked values $c_1$ and $c_2$ :

\begin{align*} & \text{All equations} \bmod n = pqr & \\ c_1 &= p^e - q^e & (1) \\ c_2 &= (p - q)^e & (2) \\ &= p^e - p^{e-1}q + \cdots - pq^{e-1} + q^e & \text{Expand} \\ c_1 + c_2 &= (p^e - q^e) + (p^e - p^{e-1}q + \cdots - pq^{e-1} + q^e) & (1) + (2) \\ &= (p^e + p^e - p^{e-1}q + \cdots - pq^{e-1}) + (q^e - q^e) & \text{Rearrange} \\ &= p (p^{e-1} + p^{e-1} - p^{e-2}q + \cdots - q^{e-1}) & \text{Factor} \\ &= k_1 p & (3) \\ c_1 - c_2 &= (p^e - q^e) - (p^e - p^{e-1}q + \cdots - pq^{e-1} + q^e) & (1) - (2) \\ &= (p^e - p^e) + (- q^e + p^{e-1}q - \cdots + pq^{e-1} - q^e) & \text{Rearrange} \\ &= q(-q^{e-1} + p^{e-1} - \cdots + pq^{e-2} - q^{e-1}) & \text{Factor} \\ &= k_2 q & (4) \\ \gcd(c_1 + c_2, n) &= \gcd(k_1 p, pqr) & \text{From} (3) \\ &= p & \\ \gcd(c_1 - c_2, n) &= \gcd(k_2 q, pqr) & \text{From} (4) \\ &= q & \\ r &= \frac{n}{pq} \\ \end{align*}

A RSA decryption key $d$ to match $e=65537 \cdot 2$ cannot be calculated since $e$ is even and therefore not is not coprime to $\phi(n)$ . However, since we know the values of $p$ , $q$ and $r$ , we can calculate the 8 possible values of $\sqrt{c} = m^{65537} \mod n$ and proceed as if $e=65537$ instead.

Exploit codesage
# ====== Parameters ======

e = 131074
n = 587926815910957928506680558951380405698765957736660571041732511939308424899531125274073420353104933723578377320050609109973567093301465914201779673281463229043539776071848986139657349676692718889679333084650490543298408820393827884588301690661795023628407437321580294262453190086595632660415087049509707898690300735866307908684649384093580089579066927072306239235691848372795522705863097316041992762430583002647242874432616919707048872023450089003861892443175057
c1 = 92883677608593259107779614675340187389627152895287502713709168556367680044547229499881430201334665342299031232736527233576918819872441595012586353493994687554993850861284698771856524058389658082754805340430113793873484033099148690745409478343585721548477862484321261504696340989152768048722100452380071775092776100545951118812510485258151625980480449364841902275382168289834835592610827304151460005023283820809211181376463308232832041617730995269229706500778999
c2 = 46236476834113109832988500718245623668321130659753618396968458085371710919173095425312826538494027621684566936459628333712619089451210986870323342712049966508077935506288610960911880157875515961210931283604254773154117519276154872411593688579702575956948337592659599321668773003355325067112181265438366718228446448254354388848428310614023369655106639341893255469632846938342940907002778575355566044700049191772800859575284398246115317686284789740336401764665472
cm = 357982930129036534232652210898740711702843117900101310390536835935714799577440705618646343456679847613022604725158389766496649223820165598357113877892553200702943562674928769780834623569501835458020870291541041964954580145140283927441757571859062193670500697241155641475887438532923910772758985332976303801843564388289302751743334888885607686066607804176327367188812325636165858751339661015759861175537925741744142766298156196248822715533235458083173713289585866

# ====== Recover key ======

p = gcd(c1 + c2, n)
print(f"{p = }")
q = gcd(c1 - c2, n)
print(f"{q = }")

r = n // p // q
print(f"{r = }")

assert p * q * r == n

phi = (p-1) * (q-1) * (r-1)
ee = e // 2
dd = ZZ(Zmod(phi)(ee) ^ -1)
print(f"{dd = }")

# ====== Manual square root then decrypt ======

from itertools import product

for rp, rq, rr in product(*[Zmod(m)(cm).sqrt(all=True) for m in [p, q, r]]):
    cmm = CRT_list([ZZ(rp), ZZ(rq), ZZ(rr)], [p, q, r])
    pt = Zmod(n)(cmm) ^ dd
    print(bytes.fromhex(hex(pt)[2:].zfill(512))[-50:])

output

p = 75724277866950572706[...]00576592403320929717
q = 86092588964302105865[...]07084038768336538857
r = 90182518745618504676[...]46165598701061994853
dd = 570020870802724838415597134387[...]230025007541067468855040422529
b"\xfd6\x86\xff$b#Ea2E\xb3!\xf8\xd3~\xc1N\x17\x87'\n\xc6b\xdbY\xca\xe7#\x9e\xd0\x96\x97'[\x18\xe0\xed\x17:\xbcb\xae[p6Ww\x11\xf7"
b'\x1e\x8d\xedm\tb\xd8\x15R\xd5\xb8\x9a\x95\xc9\x0eo\xd4\t\xc4\x12/\x06\xcc\xa5[\xa8\x17\x844\t\x8f=\x9b($\x886\x90\\|\x81\x81\x06\xb2!+\x03w\x1c('
b'\x8b(T\xdb\xc4\x8d\xad|\x14\x00\x93y\xe1j\x9d\xa0\x19\x04\xdd"\xdb\'\xe0(\xd1\xa0y\x0e\xcb1\x9b}\x9a\x13\n\xf9\xbe\xf3\x95<\xa9\x15\xb9~\xa8\t\xc3\xccW\x14'
b'\xe0\x82\xee\xdf)\xaf\xba\xb8\x9e^/\xa4$\x81\xbf\x8e\xadR>#\xa8\x9a\xa3\xd6\x1a\xee\xd8-\xb0\xf7\x8e:\x8d\x9bi\xfa\xed9\xd1\xe2\x93\xaa\xf8\xef>\x8fJ\x8b\xe8\xb4'
b'\xeby\xdd\x8bV.\xec\xda\xc8\xe7\xa7\x19\x0c7Ys\xd1\x1c\rf\x91\xee\x9e\xbf\x1c\x11\x15Py\xad=\xaf\x82\xdd\x00s:#6\xb9F\xde\x1f\xf6\xdb\xdf\xda\xb4\x8f\xdd'
b'@\xd4w\x8e\xbbP\xfa\x17SECCON{being_able_to_s0lve_this_1s_great!}'
b'\xadn\xde\xfdv{\xcf~\x14p\x1e"\x9a\xf0\n\x92\xaad\x87x\x0b\x82u\xef\xdbW\xd5\xf9\xf6\x9b<\xacuPE\xe5\xf0\xcc\xac\x1fY\x08\x123\xf9D!\xc9\\i'
b'\xce\xc6Ek[|\x84N\x06\x13\x91\n\x0e\xc0E\x83\xbd 4\x03\x13~|2[\xa6"\x97\x07\x05\xfbSyQ\x0fUFo\xf1a\x1e&j\x8a\xaa8\xcd\xc9f\x9a'

Footnotes

We can ignore the $\text{mod}$ here because it will always be less than $n$ . ↩
Ignoring some off by one errors and the case where $\text{flag} = \text{flag}_M$ . ↩