UIUCTF 2022 Crypto + Misc Writeups

Completed all the crypto challenges by 7:33:08 into the CTF and got a bunch of first bloods / first 3 solves too. The misc ML challenges were entertaining and the art gallery aesthetic was fun.

Bro-key-n
- Parsing Partial Key Parameters
- Deriving Full Key from Partial Leak
Sussy ML
blackboxwarrior
Other Challenges

Bro-key-n

By Husnain

”a shattered padlock laying in a grassy field with a rock wall in the background in a rustic style”

I tried to save my SSH key, but it seems that some of it has gotten removed! If there are any data recovery experts out there, hopefully they can recover my key…if you can, try to connect to my server to reach back to me.

ssh user@bro-key-n.chal.uiuc.tf -p 1337

Attachment: key_redacted.pem

14 solves, 408 points

First blood 🩸 at 6:27:58 from CTF start.

Challenge key_redacted.pemtext
-----BEGIN RSA PRIVATE KEY-----
MIIJJAIBAAKCAgASUWUVXgOvRLJkI77YJ6BlG5t6en55ysW40HpawMJb9bTyWMIn
NIkWpL7+swa+eddajk+sL32Fkdf38eUAbq/y0y6T/LGlDLW9RJqEhAxx+fC62Zmu
7tUA3DK3CS0LAhrd4oWdU8YE9LFhOID7StpmxaGdoFi8emZGuTXE0ooyG60KObs4
dGV3Xbwq1xhM4iG9Drw94PwOlXS5UqDNfCcY0GlrorKsUSJwjNlkPIoos5FtR7KP
Rsau1+kd8aeCeAObkZciPRqLDojy3cVXZqKO6qpXHk2qfyEy1AKAFaNyt4sEt3WY
ex9qQg9a2W0w12zD01QZnJaKhTkMhdThLHrrBQsbBPQwsjcl7FwT0DQBOPZsas+k
WUYbTr++WvKy1pB7j6eC4WUlFFKf3zQ2Z+aHXX0UmPPYDLdlJFgLbyrwEULxW7EO
kTZt2IL3c4+ywkK0F6Ty4M+lzW/Wtj0ZcpAd9pudXEgXeCSUMJ6AlU0ckOl1WSpH
zORHYZ9aPVt2Ertme7sU4XdJZLFOqXzqN1+Z96GdpUOptOmpeL2/sv/4816OlZdH
OIjLErLv73CNhxSJ592zymSZesb0rSnH4T01ResFai6HLOMvE99ezt0lt73XwyRk
MGRm0uW35Ir5rOioHkKVgas3dGjH8DED73WOrvt5p0BImSb9jyYzT9odZQIDAQAB
AoIB/0WfF5MewOJnN59kPPdRpU6kn0vkRtCg4N6PgntsJ0tdlV+F+mkIRALMJyHn
TrqmXNzSB/9ogKwqpa68tKXwDM______________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________YM4i/wJBudIGNGxwJRfOR9HUI2G/wchfC1772bxdFev5+0YM
PiuBRnypiaHcf2/AAOmDMZJFyrTqrfy8jmxfdwKCAQAMVay1pGR15Pyz/AEqJvO4
lrw09/BHA1xhDTc5uYzlChRuxJEn5ehmc1Lgbawr+jciSkfCnNkEueQYv0+EhPYF
lJBsztrCJX3hzcVEU7qJLR4aAP6Px+G0Fd/kxQVbyrCvCKM1ptmpNPqYZE2IR5Ri
Fzj4eD7rl1qEaBNIEdNs2VRMmsRwhrqIZcgRVbzcOf5cE3agelmTT/JeGFVFF+Ri
knxvhVcSScPKgsfdhpFwcYbeLqbLac7ZQcb1+Qz7XU______________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
______________________________________________________
-----END RSA PRIVATE KEY-----

Parsing Partial Key Parameters

The challenge provides a SSH private key file with some parts of its base64 data censored with underscores "_". Using the file header, we can identify it as a RSA private key encoded in the PKCS#1 format.

ipython

!wget "https://2022.uiuc.tf/files/6ba91c25ec2929bb9dd73ec46a815b43/key_redacted.pem?token=no-u" -O key_redacted.pem 2>/dev/null

with open("key_redacted.pem", "r") as f:
    raw = f.read()

print("Redacted key:")
print(raw)

output

Redacted key:
-----BEGIN RSA PRIVATE KEY-----
MIIJJAIBAAKCAgASUWUVXgOvRLJkI77YJ6BlG5t6en55ysW40HpawMJb9bTyWMIn
NIkWpL7+swa+eddajk+sL32Fkdf38eUAbq/y0y6T/LGlDLW9RJqEhAxx+fC62Zmu
[... 9 lines ...]
AoIB/0WfF5MewOJnN59kPPdRpU6kn0vkRtCg4N6PgntsJ0tdlV+F+mkIRALMJyHn
TrqmXNzSB/9ogKwqpa68tKXwDM______________________________________
________________________________________________________________
[... 16 lines ...]
________________________________________________________________
________________YM4i/wJBudIGNGxwJRfOR9HUI2G/wchfC1772bxdFev5+0YM
PiuBRnypiaHcf2/AAOmDMZJFyrTqrfy8jmxfdwKCAQAMVay1pGR15Pyz/AEqJvO4
lrw09/BHA1xhDTc5uYzlChRuxJEn5ehmc1Lgbawr+jciSkfCnNkEueQYv0+EhPYF
lJBsztrCJX3hzcVEU7qJLR4aAP6Px+G0Fd/kxQVbyrCvCKM1ptmpNPqYZE2IR5Ri
Fzj4eD7rl1qEaBNIEdNs2VRMmsRwhrqIZcgRVbzcOf5cE3agelmTT/JeGFVFF+Ri
knxvhVcSScPKgsfdhpFwcYbeLqbLac7ZQcb1+Qz7XU______________________
________________________________________________________________
[... 9 lines ...]
________________________________________________________________
______________________________________________________
-----END RSA PRIVATE KEY-----

We should try to unpack whatever parameters we have remaining after the censor with some careful handling of the base64 data. One consideration is that the base64 might have had its padding = characters censored, so we will need to manually repair this as well. We derive one version of the key key_bytes with all censored bits set to zero. We also another version of the key key_mask that sets all provided bits set to 1 to differentiate between data that is known and data that is censored.

python

import base64

key_b64 = "".join(raw.split("\n")[1:-1])
key_bytes = base64.b64decode(
    key_b64.replace("_", "A")[:-2] + "=="
)
key_mask = base64.b64decode(
    "".join([
        "/" if i != "_" else "A"
        for i in key_b64
    ])[:-2] + "=="
)

print("Key length:", len(key_bytes))
print("Key hex   :", key_bytes.hex())
print("Key mask  :", key_mask.hex())

output

Key length: 2343
Key hex   : 30820924[...1175 nibbles...]4a5f00cc00000000[...1793 0s...]0000000060ce22ff[...503 nibbles...]90cfb5d400000000[...1151 0s...]00000000
Key mask  : ffffffff[...1175 nibbles...]ffffffff00000000[...1793 0s...]00000000ffffffff[...503 nibbles...]ffffffff00000000[...1151 0s...]00000000

With some help from reference documents, we can make a custom parser for DER encoding. In brief, the binary format is made of “chunks” with a header and data component:

text

1 byte             - Tag / "data type"
1 byte             - Short Length
2+ bytes, optional - Extended Length, use if Short Length > 127
[Length] bytes     - Raw data

The tag 0x02 means the chunk data should be unpacked as an integer while the tag 0x30 means the chunk data should be re-parsed as a “Sequence” of DER struct chunks.

If we try to decode the key data, the output from our custom parser looks very broken.

python

def der_unpack(bytes_stream):
    take_pos = 0
    def take(n_bytes, to_int=True):
        nonlocal take_pos
        res = bytes_stream[take_pos:take_pos + n_bytes]
        take_pos += n_bytes

        if to_int:
            res = int("0" + res.hex(), 16)
        return res, (take_pos - n_bytes, take_pos)

    tag, _ = take(1)
    length, _ = take(1)
    if length > 127:
        length, _ = take(length & 0x7f)

    print("Tag:", hex(tag), "Length:", length)

    res = None

    if tag == 0x30:
        res = []
        inner_data, _ = take(length, to_int=False)
        inner_pos = 0
        while inner_pos < length:
            inner_res, inner_used = der_unpack(inner_data[inner_pos:])
            res.append(inner_res)
            inner_pos += inner_used
    elif tag == 0x02:
        res, _ = take(length)

    return res, take_pos

unpacked_one, _ = der_unpack(key_bytes)
unpacked_one

output

Tag: 0x30 Length: 2340
Tag: 0x2 Length: 1
Tag: 0x2 Length: 512
Tag: 0x2 Length: 3
Tag: 0x2 Length: 511
Tag: 0x0 Length: 0
Tag: 0x0 Length: 0
[... 225 lines ...]
Tag: 0x0 Length: 0
Tag: 0x0 Length: 96
Tag: 0xce Length: 34
Tag: 0xff Length: 2
Tag: 0x41 Length: 152653748797832928540701597108483994378953966160680445744167340574148103854442783338494896727469832286558098117778098613026785699650363255
Tag: 0x2 Length: 256
Tag: 0x0 Length: 0
Tag: 0x0 Length: 0
[... 257 lines ...]
Tag: 0x0 Length: 0

[0,
    7473071059429749799883[... 1200 digits ...]8086142309,
    65537,
    1109495115862054496740[... 1200 digits ...]268622848,
    None,
    None,
[... 229 lines ...]
    None,
    1557107402445517512071[... 580 digits ...]90411828461568,
    None,
    None,
[... 257 lines ...]
    None]

Some of the Short Length / Extended Length headers were censored, meaning the parser does not know where to start and stop unpacking integers. Despite this, we have recovered n and e of the RSA key successfully. These two parameters are the first few in the key their lengths were not censored, so they were correctly parsed.

python

print("n?   :", unpacked_one[1])
print("e?   :", unpacked_one[2])
print("nbits:", unpacked_one[1].bit_length())

output

n?   : 74730710594297497998834917292958574326261570046287129781931934054213111306254334128256880161501261431036308866307401809598884203048119260022950758640396195299559686696801568698277234662263784791646957402901562704843369944910137198210590728027494147492081069047601914153683009607246904324318006267281728061068765198409492115406429903240201986799412205619539503903333646153924746128370306308919783546917794469142114909529332967288762837204316066670076604177246814072186481514252837380462674562538731078616331087438285141193830486276452225784277750468369140593630278298364856437080663606193901885059609612156491256300459756387056772426043293214632648749536402338342023322162531903580529852119776102132401250459874163729498714887772294526014311193101002569051675808202046766617978226091095698514584760534070607724116707487082132910493877383878640627671196638761172332957356224913669643653466835649744015103051054359296315300402283360191484498795911245330651493449853357321588056066131726948480894983250183011703385805884787067991538150892246705241586180276540601217315435289876906708500231461260708209542391993558735232736456215096566103990848282646890317408863427045373525008472036542870689170016355686709136857446938045299448086142309
e?   : 65537
nbits: 4093

To determine the lengths of the parameters, we can generate a dummy key with same bit length and parse that to get a known working tag/chunk layout.

ipython

!ssh-keygen -b 4093 -m pem -f demo_key.pem -N "" <<< y

with open("demo_key.pem", "r") as f:
    demo_raw = f.read()

demo_b64 = "".join(demo_raw.split("\n")[1:-1])
demo_bytes = base64.b64decode(
    demo_b64.replace("_", "A")
)

unpacked_demo, _ = der_unpack(demo_bytes)
unpacked_demo

output

Generating public/private rsa key pair.
demo_key.pem already exists.
Overwrite (y/n)? Your identification has been saved in demo_key.pem
Your public key has been saved in demo_key.pem.pub
The key fingerprint is:
SHA256:inFQrLVTy/XJR2i1WzReWqX5o5ER0UoLR3ef10CCGzw sy@SYVAPOR
The key's randomart image is:
+---[RSA 4093]----+
|     ..  . .oB*oB|
|     .o . E.o+=XB|
|    .o + o B++Bo=|
|    ..o o . +o++.|
|    . ..S    +...|
|     + .      o .|
|    . .      .   |
|                 |
|                 |
+----[SHA256]-----+
Tag: 0x30 Length: 2340
Tag: 0x2 Length: 1
Tag: 0x2 Length: 512
Tag: 0x2 Length: 3
Tag: 0x2 Length: 512
Tag: 0x2 Length: 256
Tag: 0x2 Length: 256
Tag: 0x2 Length: 256
Tag: 0x2 Length: 256
Tag: 0x2 Length: 256

[0,
    9622395594545263753511[... 1200 digits ...]6755577479,
    65537,
    7294503226089045787905[... 1200 digits ...]2918758097,
    1322935933887554560075[... 580 digits ...]594486269046053,
    7273515933813267674448[... 580 digits ...]23734542192443,
    1310804092389371544517[... 580 digits ...]325092090983329,
    5031652225327557205188[... 580 digits ...]58325113132715,
    9507348386917704126798[... 580 digits ...]15158535783249]

We can modify the DER parser to use these known working chunk tags and data lengths and use that with the censored key. We manually set one chunk to length 511 since we know that length is valid from earlier.

However, the parser is still a bit broken. One chunk reports an invalid tag of 0x77, but all tags should either be 0x02 if the header was not censored or 0x00 if the header was censored. There also seems to be data left over at the end after parsing the DER sequence which throws an error unless we add one dummy chunk at the end.

python

fixed_tag_length = [
    (0x30, 2340), (0x02, 1), (0x02, 512), (0x02, 3), (0x02, 511),
    (0x02, 256), (0x02, 256), (0x02, 256), (0x02, 256), (0x02, 256),

    # this shouldn't be here
    (0xff, 9999)
]

def der_unpack_fixed(bytes_stream):
    global fixed_tag_length

    take_pos = 0
    def take(n_bytes, to_int=True):
        nonlocal take_pos
        res = bytes_stream[take_pos:take_pos + n_bytes]
        take_pos += n_bytes

        if to_int:
            res = int("0" + res.hex(), 16)
        return res, (take_pos - n_bytes, take_pos)

    (tag, length), fixed_tag_length = fixed_tag_length[0], fixed_tag_length[1:]
    actual_tag, _ = take(1) # tag
    take(1) # length
    if length > 127:
        take(2) # extended length

    print("Tag:", hex(tag), "Length:", length, "Actual tag:", hex(actual_tag))

    res = None

    if tag == 0x30:
        res = []
        inner_data, _ = take(length, to_int=False)
        inner_pos = 0
        while inner_pos < length:
            inner_res, inner_used = der_unpack_fixed(inner_data[inner_pos:]) # new recursion
            res.append(inner_res)
            inner_pos += inner_used
    elif tag == 0x02:
        res, _ = take(length)

    return res, take_pos

unpacked_two, _ = der_unpack_fixed(key_bytes)
unpacked_two

output

Tag: 0x30 Length: 2340 Actual tag: 0x30
Tag: 0x2 Length: 1 Actual tag: 0x2
Tag: 0x2 Length: 512 Actual tag: 0x2
Tag: 0x2 Length: 3 Actual tag: 0x2
Tag: 0x2 Length: 511 Actual tag: 0x2
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x77
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0xff Length: 9999 Actual tag: 0x0

[0,
    7473071059429749799883[... 1200 digits ...]8086142309,
    65537,
    1109495115862054496740[... 1200 digits ...]268622848,
    0,
    1980508142803874403456[... 120 digits ...]8400973919,
    6082450790802802781530[... 580 digits ...]00046204928,
    0,
    0,
    None]

After inspecting the censored key hex¹, we discover that this is because one of the parameters in censored key has a 1 byte longer field compared to the known working key. One of the early parameters should have a length of 257 instead of 256. After making this change, we can successfully parse the censored key.

python

fixed_tag_length = [
    (0x30, 2340), (0x02, 1), (0x02, 512), (0x02, 3), (0x02, 511),
    # Change to 257 to align chunks
    (0x02, 257),
    (0x02, 256), (0x02, 256), (0x02, 256), (0x02, 256)
]

unpacked_final, _ = der_unpack_fixed(key_bytes)
unpacked_final

output

Tag: 0x30 Length: 2340 Actual tag: 0x30
Tag: 0x2 Length: 1 Actual tag: 0x2
Tag: 0x2 Length: 512 Actual tag: 0x2
Tag: 0x2 Length: 3 Actual tag: 0x2
Tag: 0x2 Length: 511 Actual tag: 0x2
Tag: 0x2 Length: 257 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x2
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0

[0,
    7473071059429749799883[... 1200 digits ...]8086142309,
    65537,
    1109495115862054496740[... 1200 digits ...]268622848,
    0,
    5070100845577918472847[... 120 digits ...]190649323383,
    1557107402445517512071[... 580 digits ...]90411828461568,
    0,
    0]

Run the parser once more with the key_mask from earlier so we obtain the bitmask of uncensored. We can refer to some pyrcyptodome source to find the order that the parameters appear in a private key. The next step is to recover the full key from this partial key leak.

python

fixed_tag_length = [
    (0x30, 2340), (0x02, 1), (0x02, 512), (0x02, 3), (0x02, 511),
    (0x02, 257), (0x02, 256), (0x02, 256), (0x02, 256), (0x02, 256)
]

unpacked_mask, _ = der_unpack_fixed(key_mask)

param_names = ["ver", "n", "e", "d", "p", "q", "dp", "dq", "qinv"]
for param_name, param, param_mask in zip(param_names, unpacked_final, unpacked_mask):
    if param_mask == 0:
        print(param_name, ": ?")
        continue
    print(param_name, ":")
    param = hex(param)[2:]
    param_mask = hex(param_mask)[2:]
    param = param.zfill(len(param_mask))
    print(param)
    print(param_mask)

output

Tag: 0x30 Length: 2340 Actual tag: 0xff
Tag: 0x2 Length: 1 Actual tag: 0xff
Tag: 0x2 Length: 512 Actual tag: 0xff
Tag: 0x2 Length: 3 Actual tag: 0xff
Tag: 0x2 Length: 511 Actual tag: 0xff
Tag: 0x2 Length: 257 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0xff
Tag: 0x2 Length: 256 Actual tag: 0x0
Tag: 0x2 Length: 256 Actual tag: 0x0

ver :
00
ff
n :
125165155e03af44b26423bed827a0651b9b7a7a7e79cac5b8d07a5ac0c25bf5b4f258c227348916a4befeb306be79d75a8e4fac2f7d8591d7f7f1e5006eaff2d32e93fcb1a50cb5bd449a84840c71f9f0bad999aeeed500dc32b7092d0b021adde2859d53c604f4b1613880fb4ada66c5a19da058bc7a6646b935c4d28a321bad0a39bb387465775dbc2ad7184ce221bd0ebc3de0fc0e9574b952a0cd7c2718d0696ba2b2ac5122708cd9643c8a28b3916d47b28f46c6aed7e91df1a78278039b9197223d1a8b0e88f2ddc55766a28eeaaa571e4daa7f2132d4028015a372b78b04b775987b1f6a420f5ad96d30d76cc3d354199c968a85390c85d4e12c7aeb050b1b04f430b23725ec5c13d0340138f66c6acfa459461b4ebfbe5af2b2d6907b8fa782e1652514529fdf343667e6875d7d1498f3d80cb76524580b6f2af01142f15bb10e91366dd882f7738fb2c242b417a4f2e0cfa5cd6fd6b63d1972901df69b9d5c4817782494309e80954d1c90e975592a47cce447619f5a3d5b7612bb667bbb14e1774964b14ea97cea375f99f7a19da543a9b4e9a978bdbfb2fff8f35e8e9597473888cb12b2efef708d871489e7ddb3ca64997ac6f4ad29c7e13d3545eb056a2e872ce32f13df5ecedd25b7bdd7c32464306466d2e5b7e48af9ace8a81e429581ab377468c7f03103ef758eaefb79a740489926fd8f26334fda1d65
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
e :
010001
ffffff
d :
459f17931ec0e267379f643cf751a54ea49f4be446d0a0e0de8f827b6c274b5d955f85fa69084402cc2721e74ebaa65cdcd207ff6880ac2aa5aebcb4a5f00cc0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
p : ?
q :
60ce22ff0241b9d206346c702517ce47d1d42361bfc1c85f0b5efbd9bc5d15ebf9fb460c3e2b81467ca989a1dc7f6fc000e983319245cab4eaadfcbc8e6c5f77
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
dp :
0c55acb5a46475e4fcb3fc012a26f3b896bc34f7f047035c610d3739b98ce50a146ec49127e5e8667352e06dac2bfa37224a47c29cd904b9e418bf4f8484f60594906ccedac2257de1cdc54453ba892d1e1a00fe8fc7e1b415dfe4c5055bcab0af08a335a6d9a934fa98644d884794621738f8783eeb975a8468134811d36cd9544c9ac47086ba8865c81155bcdc39fe5c1376a07a59934ff25e18554517e462927c6f85571249c3ca82c7dd8691707186de2ea6cb69ced941c6f5f90cfb5d4000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
dq : ?
qinv : ?

Deriving Full Key from Partial Leak

In summary, we know:

All of n and e
High 127 nibbles of d, missing low 895 nibbles
Low 127 nibbles of q, missing high 384 nibbles
High 382 nibbles of dp, missing low 129 nibbles

python

n = 0x125165155e03af44b26423bed827a0651b9b7a7a7e79cac5b8d07a5ac0c25bf5b4f258c227348916a4befeb306be79d75a8e4fac2f7d8591d7f7f1e5006eaff2d32e93fcb1a50cb5bd449a84840c71f9f0bad999aeeed500dc32b7092d0b021adde2859d53c604f4b1613880fb4ada66c5a19da058bc7a6646b935c4d28a321bad0a39bb387465775dbc2ad7184ce221bd0ebc3de0fc0e9574b952a0cd7c2718d0696ba2b2ac5122708cd9643c8a28b3916d47b28f46c6aed7e91df1a78278039b9197223d1a8b0e88f2ddc55766a28eeaaa571e4daa7f2132d4028015a372b78b04b775987b1f6a420f5ad96d30d76cc3d354199c968a85390c85d4e12c7aeb050b1b04f430b23725ec5c13d0340138f66c6acfa459461b4ebfbe5af2b2d6907b8fa782e1652514529fdf343667e6875d7d1498f3d80cb76524580b6f2af01142f15bb10e91366dd882f7738fb2c242b417a4f2e0cfa5cd6fd6b63d1972901df69b9d5c4817782494309e80954d1c90e975592a47cce447619f5a3d5b7612bb667bbb14e1774964b14ea97cea375f99f7a19da543a9b4e9a978bdbfb2fff8f35e8e9597473888cb12b2efef708d871489e7ddb3ca64997ac6f4ad29c7e13d3545eb056a2e872ce32f13df5ecedd25b7bdd7c32464306466d2e5b7e48af9ace8a81e429581ab377468c7f03103ef758eaefb79a740489926fd8f26334fda1d65
e = 0x10001

# d = d_high * (2 ** (895 * 4)) + d_low
d_high = 0x459f17931ec0e267379f643cf751a54ea49f4be446d0a0e0de8f827b6c274b5d955f85fa69084402cc2721e74ebaa65cdcd207ff6880ac2aa5aebcb4a5f00cc
# d_low < 2 ** (895 * 4)

# q = q_high * (2 ** (128 * 4)) + q_low
# q_high < 2 ** (384 * 4)
q_low = 0x60ce22ff0241b9d206346c702517ce47d1d42361bfc1c85f0b5efbd9bc5d15ebf9fb460c3e2b81467ca989a1dc7f6fc000e983319245cab4eaadfcbc8e6c5f77

# dp = dp_high * (2 ** (129 * 4)) + dp_low
dp_high = 0xc55acb5a46475e4fcb3fc012a26f3b896bc34f7f047035c610d3739b98ce50a146ec49127e5e8667352e06dac2bfa37224a47c29cd904b9e418bf4f8484f60594906ccedac2257de1cdc54453ba892d1e1a00fe8fc7e1b415dfe4c5055bcab0af08a335a6d9a934fa98644d884794621738f8783eeb975a8468134811d36cd9544c9ac47086ba8865c81155bcdc39fe5c1376a07a59934ff25e18554517e462927c6f85571249c3ca82c7dd8691707186de2ea6cb69ced941c6f5f90cfb5d4
# dp_low < 2 ** (129 * 4)

Since $n = p * q$ we can use $p = n \cdot q^{-1} \mod 2^{128 \cdot 4}$ to recover the low 128 nibbles of p. This works since p and q are prime and therefore all variables involved are coprime to $2^{128 \cdot 4}$ .

python

two_pow_512 = 2 ** 512

# p = p_high * (2 ** (128 * 4)) + p_low
# p_high < 2 ** (384 * 4)
p_low = n * pow(q_low, -1, two_pow_512) % two_pow_512

print("p_low:", hex(p_low))

output

p_low: 0x4de489a6bbda0dfbf05ff3c234c1a2c365f7dd48fa1978a800d944248d6896f9838b2d5187bcd2a39cac9a0603daf5b47351e7912412dca7598c1ac51f28b903

Since we know many bits of dp_high and have a closely associated value p_low, we can rearrange some equations $d = d_p \mod (p-1)$ and $e \cdot d = 1 \mod (p-1) \cdot (q-1)$ to get an equation relating variables $d_{p\,\text{low}}$ , $p_{\text{high}}$ and $k$ .

\begin{align*} d &= d_p \mod (p-1) & \text{(1)} \\ e \cdot d &= 1 \mod (p-1) \cdot (q-1) & \text{(2)} \\ e \cdot d &= 1 \mod p-1 & \text{Change mod of (2)} \\ e \cdot d_p &= 1 \mod p-1 & \text{Sub (1)} \\ e \cdot d_p &= 1 + k \cdot (p-1) & \text{Expand mod} \\ e \cdot (d_{p\,\text{high}} \cdot 2^{129 \cdot 4} + d_{p\,\text{low}}) &= 1 + k \cdot (p_{\text{high}} * 2^{128 \cdot 4} + p_{\text{low}} - 1) & \text{Expand high/low} \\ \end{align*} \\ \text{where} \, 0 < d_{p\,\text{low}} < 2^{129 \cdot 4} \, , \, 0 < p_{\text{high}} < 2^{384 \cdot 4} \, \text{and} \, 0 < k < e

Since $0 < k < e$ , we can iterate through all possible values of $k$ to look for integer solutions to the other two variables $d_{p\,\text{low}}$ and $p_{\text{high}}$ . We use z3 to find possible solutions to the equation and afterwards check manually if we find a $p$ which divides $n$ . After optionally speeding up processing with multithreading, around half an hour of CPU time is needed to get a valid $p$ .

python

import multiprocessing
from z3 import *
from Crypto.Util.number import isPrime
from tqdm.auto import tqdm

dp_high_offset = 2 ** (129 * 4)
dp_low_limit = 2 ** (129 * 4)
p_high_offset = 2 ** (128 * 4)
p_high_limit = 2 ** (384 * 4)

def solve_k(k):
    dp_low = Int("dp_low")
    p_high = Int("p_high")

    s = Solver()
    s.add(
      e * (dp_high * dp_high_offset + dp_low) ==
      1 + k * (p_high * p_high_offset + p_low - 1)
    )
    s.add(0 < dp_low, dp_low < dp_low_limit)
    s.add(0 < p_high, p_high < p_high_limit)

    res = s.check()
    if str(res) == "unsat":
        return False

    model = s.model()
    p = model[p_high].as_long() * two_pow_512 + p_low
    dp = dp_high * dp_high_offset + model[dp_low].as_long()
    assert e * dp % (p-1) == 1

    if not isPrime(p):
        return False
    print("!!!")
    print("k:", k)
    print("p:", p)
    return p

p = None

# jobs = list(range(0, e + 1))
# skip to the interesting part for the writeup
jobs = list(range(27500, e + 1))
with multiprocessing.Pool(4) as p:
    for res in tqdm(p.imap(solve_k, jobs), total=len(jobs)):
        if res:
            p = res
            break

output

    0%|          | 0/38038 [00:00<?, ?it/s]

!!!
k: 28128
p: 3627991603884808062736141310447106260943326330899396275199779984022462194376994246446102117532813224234792046840726872009503786329408256663119027353255969224649727885389580250774873824390822482215139013309728202469835336298188620697403248917907049738004864552884412233025397042416703298163382725246031075810130222032765486555500736412969415261015967808462136504839813036078699995347830504646364842806157413675646357345753021818180743963892741139070590339137165833818468345693182851348835784086931651709553805159969447778964285167310407227065749316889692916103874856521269259363246539154909931419853080560118329293059

With known $p$ , we can recover $q$ and the rest of the RSA key parameters. Export the key into a valid PEM file and diff with the redacted key to see that the original uncensored data has not changed, confirming that the key is good.

python

from Crypto.PublicKey import RSA

print(f"{n % p == 0 = }")
q = n // p
print(f"{p * q == n = }")

phi = (p-1) * (q-1)
d = pow(e, -1, phi)
rsa_key = RSA.construct((n, e, d, p, q))
rsa_key_bytes = rsa_key.export_key("PEM")

with open("key_solved.pem", "wb") as f:
    f.write(rsa_key_bytes)

output

n % p == 0 = True
p * q == n = True

ipython

!diff key_redacted.pem key_solved.pem

diff

14,33c14,33
< TrqmXNzSB/9ogKwqpa68tKXwDM______________________________________
< ________________________________________________________________
< ________________________________________________________________
[... 15 lines ...]
< ________________________________________________________________
< ________________YM4i/wJBudIGNGxwJRfOR9HUI2G/wchfC1772bxdFev5+0YM
---
> TrqmXNzSB/9ogKwqpa68tKXwDM3f2iidRpMKu7WiCaegO6z3Sv7iDjvTg8DBLACB
> 37D3TyYGz9Anl3k+jO/20kRJO89hV+LCjoHOtOwZBUQO8zF//y/ePLdVrlEA8y3g
> WXvd/l2So+SMOXc0lW/JnWNjfTXS6tsuhepqdXtR2vAfKP2JgjLXTtNBLeVcu6oT
[... 15 lines ...]
> Jr8vG1yp69lsJ/RqkfD3aqCVkKyAh0kQsxwjOcx/mAIbJVFrZ4lSUfwbWkwvb4Sn
> VeFtuQA2OfeHo3zNYM4i/wJBudIGNGxwJRfOR9HUI2G/wchfC1772bxdFev5+0YM
38,50c38,50
< knxvhVcSScPKgsfdhpFwcYbeLqbLac7ZQcb1+Qz7XU______________________
< ________________________________________________________________
[... 9 lines ...]
< ________________________________________________________________
< ______________________________________________________
---
> knxvhVcSScPKgsfdhpFwcYbeLqbLac7ZQcb1+Qz7XUnrZIsv5LBSEC+6/wP7YKBa
> /QjFEO1GwWJZ+uYkSgz5v12V/n1fpMtDLZtm/+3nrE0msaCRysnNqoXkfBjeprvB
[... 9 lines ...]
> iZoKtTj3kUZygpfBT8/99gAm1Gmm4vxEUqpZ3hxybBGGmE1J41gN/kPdyOuoM+S3
> y6IZWpdwDrjZI8GJWqQE8xSzuWdKKFU6e+/rQumzIFYN/zTYJdnZxw==

Finally, we can use the SSH key to claim the flag.

ipython

!chmod 600 key_solved.pem
!ssh -i key_solved.pem user@bro-key-n.chal.uiuc.tf -p 1337

output

Congratulations! You found my key - if you take a look at it carefully, you'll find the flag - replace slashes in the key with underscores to get your flag...:
uiuctf{hidden_in_plain_sight}
Connection to bro-key-n.chal.uiuc.tf closed.

And just like the server says, the flag is actually visible inside the PEM file if you look hard enough.

ipython

!grep uiuc key_solved.pem

output

Fzua/uiuctf/hidden/in/plain/sight///0nw3crWsTXmP0JYEVjhNATT3RvGE

Sussy ML

By SahilJain

”suspicious machine learning model secretly among us”

Top scientists in Among Us have finally delivered the impossible; A method to classify the SUS with perfect accuracy. To solve amogus once and for all, they needed to suss out the sus at scale, and thus created a Neural Network classifier for crewmate images that achieved 100% accuracy over the population, which has a ‘sus’ rate of less than 5%.

However, among the us lurked a final sus, who destroyed the back half of the fully trained model (where the classification head and some convolutional layers were), and now the sus epidemic looms large again.

With the partial model left over from the fully trained model, figure out; Who. Is. Sus?

Flag format is uiuctf{n1_n2_n3_...} where n# is the numbers that are sus sorted in ascending order. Each image has a number in the filename. For example, if 001.png, 005.png, and 010.png are sus, the flag would be uiuctf1510

Attachment: sussy.tar.gz

18 solves, 371 points

Challenge sussy.pypython
import torch
import torch.nn as nn
import torchvision
import torch.nn.functional as F
import os
from PIL import Image

IMAGE_DIR = './crewmates/'
MODEL_PATH = './partial_sus_detector.pt'

# load all images into memory
def load_images(path):
    images = []
    paths = []
    for filename in os.listdir(path):
        paths.append(filename)
    paths.sort()

    for filename in paths:
        im = Image.open(path + filename)
        images.append(im)

    transforms = torchvision.transforms.ToTensor()
    players = [transforms(image) for image in images]
    players = torch.stack(players)
    return players

# A partial classifier
class PartialModel(nn.Module):
    def __init__(self, input_channels):
        super(PartialModel, self).__init__()
        self.conv1 = nn.Conv2d(input_channels, 32, 3, padding=1)
        self.conv2 = nn.Conv2d(32, 32, 3, padding=1)
        self.conv3 = nn.Conv2d(32, 32, 3, padding=1)
        self.conv4 = nn.Conv2d(32, 64, 3, padding=1)
        self.pooling = nn.MaxPool2d(2, 2)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.pooling(x)
        x = F.relu(self.conv2(x))
        x = self.pooling(x)
        x = F.relu(self.conv3(x))
        x = F.relu(self.conv4(x))
        x = self.pooling(x)
        return x

partial_model = PartialModel(3)
partial_model.load_state_dict(torch.load(MODEL_PATH))
partial_model.eval()

crewmates = load_images(IMAGE_DIR)

partial_outputs = partial_model(crewmates)

The challenge provides pretrained model weights, 222 images of testing data and a sample script to run a machine learning model. However, the model abruptly ends at a pooling layer and outputs a $64 \times 4 \times 4 = 1024$ wide embedding output per image instead of classifying “not sus” and “sus”. Given that the “sus” label is rare with expected less than $222 * 0.05 \approx 11$ images being “sus”, we can instead run some kind of outlier detection on the output embeddings.

The first job would be to actually get the partial model outputs. You can install pytorch on your local machine, but since the model was small I chose to use a Google Colab IPython kernel since it would be simple to set up.

ipython

!wget "https://2022.uiuc.tf/files/5192468fcb391b416df428e74a006bfc/sussy.tar.gz?token=no-u" -O sussy.tar.gz 2>/dev/null
!tar -xf sussy.tar.gz
!mv sus_classifier/* .

from sussy import *

print("Partial output shape:")
print(partial_outputs.shape)
print("Partial output:")
print(partial_outputs)

output

Partial output shape:
torch.Size([222, 64, 4, 4])
Partial output:
tensor([[[[0.0000, 0.0000, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 0.0000]],
          ...,
         [[0.0418, 0.0419, 0.0420, 0.0426],
          [0.0419, 0.0418, 0.0418, 0.0418],
          [0.0418, 0.0418, 0.0418, 0.0418],
          [0.0418, 0.0418, 0.0418, 0.0419]]]],
       grad_fn=<MaxPool2DWithIndicesBackward0>)

To find outliers, we need to convert each image’s $1024$ -dimension output embedding to a $1$ -dimension “sus”-ness value; this is called dimensionality reduction. Some straightforward ways to do this would be using sklearn’s principal component analysis or isomap models, both of which are robust enough to lead to the flag. For this writeup, I use the Isomap model to convert the large input to a $1$ -dimension value and visualise this with a histogram plot.

python

from sklearn.manifold import Isomap
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

partial_outputs_np = partial_outputs.detach().numpy()
partial_outputs_np_flat = partial_outputs_np.reshape((222, 64 * 4 * 4))
iso = Isomap(n_components=1)
one_dimension_embedding = iso.fit_transform(partial_outputs_np_flat)[:, 0]
plt.hist(one_dimension_embedding)

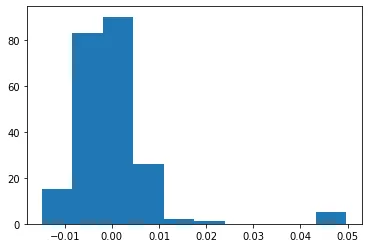
The distribution has two peaks; the smaller peak to the right looks like outliers and are likely from the “sus” images. We can filter for the images which had a value of $>0.35$ and use those to generate the flag.

python

sus_labels = np.where(one_dimension_embedding > 0.035)[0].tolist()
flag = "uiuctf{" + "_".join(str(i) for i in sorted(sus_labels)) + "}"
print("flag:", flag)

output

flag: uiuctf{2_31_41_59_65}

We can confirm the flag is correct by submitting it to the CTF platform.

blackboxwarrior

By helloca, ian5v

”art thief stealing art in the style of Van Gogh”

pull off the most daring heist in art history! transfer enough art out of the museum to pull off a successful attack. be careful not to deface the art too badly, or the heist loses all value!

link: https://blackbox-web.chal.uiuc.tf/

Attachment: app.py

22 solves, 332 points

Challenge is broken. Submitting the challenge images back would pass the machine learning check because it would compare a number label against a text label, bypassing the entire classification check and giving out flag for free.

However, I think I did an intended solve, so…

PATCHED Challenge app.pypython
#the more things change, the more they stay the same ;)
#if this looks familiar, it is! welcome back, good luck, have fun
import io
import os
import random
import base64
import json
from flask import Flask, jsonify, request, render_template, session
from flask_kvsession import KVSessionExtension
import numpy as np

from sqlalchemy import create_engine, MetaData
from simplekv.db.sql import SQLAlchemyStore
from datetime import timedelta

from werkzeug.utils import secure_filename
from werkzeug.exceptions import HTTPException
from PIL import Image
import imagehash

from torchvision.models import efficientnet_b0
import torchvision.transforms as transforms
import torchvision
import torch.nn as nn
import torch

# Use environment variable if it exists
FLAG = os.environ.get("FLAG", "uiuctf{fake_flag}")
MIN_LEVEL = 50
SESSION_MINUTES = 5
MUST_REPEAT_CAPTCHA = True
HASH_DIFFERENCE = 4 # how different the imagehash is

app = Flask(__name__)
app.config['SECRET_KEY'] = os.urandom(64)

# Store local session
engine = create_engine('sqlite:////tmp/sessions.db')
metadata = MetaData(bind=engine)
store = SQLAlchemyStore(engine, metadata, 'kvsession_table')
metadata.create_all()
kvsession_extension = KVSessionExtension(store, app)

app.permanent_session_lifetime = timedelta(minutes=SESSION_MINUTES)

# ------------------ Model goes here ⬇------------------ #
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# model = secret_model()
# !!! PATCH: I made my own model file trained on 4 epochs of the CIFAR10 train dataset
#            but we solve the challenge without needing to know this
model = efficientnet_b0(num_classes=len(classes))
model.load_state_dict(torch.load("../models/model.pth", map_location = device))
model = model.to(device)
model.eval()

image_set = torchvision.datasets.CIFAR10(root='./static/images', train=False, download=True)
# ------------------ Model goes here ------------------ #

# Get a random image and show it to the user
def gen_img():
    label = 0
    curr_image, label = image_set[random.randint(1, len(image_set))]
    resize_images = transforms.Compose([transforms.Resize(256),
                        transforms.CenterCrop(224)])
    curr_image = resize_images(curr_image)

    buffered = io.BytesIO()
    curr_image.save(buffered, format='png')
    # return base64.b64encode(buffered.getvalue()).decode('utf-8'), label
    # !!! PATCH: Return a string label instead
    return base64.b64encode(buffered.getvalue()).decode('utf-8'), classes[label]

# Transform image to normalize into model's bounds
def transform_image(image_bytes):
    my_transforms = transforms.Compose([
                        transforms.ToTensor(),
                        transforms.Normalize(
                            [0.485, 0.456, 0.406],
                            [0.229, 0.224, 0.225])])
    image = Image.open(io.BytesIO(image_bytes))
    return my_transforms(image).unsqueeze(0)


def tensor_to_image(tensor):
    tensor = tensor.detach().squeeze().numpy()
    tensor = tensor.transpose(1, 2, 0)
    tensor = (tensor * 255).astype(np.uint8)
    return Image.fromarray(tensor)

def image_to_tensor(img):
    tensor = np.array(img).astype(np.float32) / 255.0
    tensor = tensor.transpose(2, 0, 1)
    tensor = tensor[None, :, :, :]
    return torch.tensor(tensor, requires_grad=True)

def bytes_to_image(img_data):
    import tempfile
    with tempfile.NamedTemporaryFile(suffix='.png') as tmp:
        tmp.write(img_data)
        tmp.flush()
        return Image.open(tmp.name)

def get_prediction(image_bytes, model, curr_image = None):
    inputs = transform_image(image_bytes=image_bytes)
    outputs = model(inputs)
    preds = torch.argmax(outputs, 1)
    original = Image.open(io.BytesIO(base64.b64decode(curr_image)))

    input_image = Image.open(io.BytesIO(image_bytes))
    hash_orig = imagehash.average_hash(original)
    hash_input = imagehash.average_hash(input_image)

    if hash_orig - hash_input < HASH_DIFFERENCE:
        return classes[preds]
    else:
        return "IMAGE WAS TOO DIFFERENT"

# Function that takes care of the website's repeated image generation and edge conditions
@app.route('/', methods=['GET', 'POST'])
def index():

    response = None
    img = None
    regen_image = session.get('img') is None

    if session.get('level') is None:
        session['level'] = 0
        session['yolo'] = 0
        session.permanent = True

    if request.method == 'POST' and 'img' in session:
        file = request.files['file']
        img_bytes = file.read()

        image = bytes_to_image(img_bytes)
        (width, height) = image.size
        depth = len(image.getbands())

        if width != 224 or height != 224 or depth != 3:
            response = f"Invalid image shape. Expecting 224 x 224 with 3 channels, got {width} x {height} with {depth} channels"
        else:
            pred = get_prediction(image_bytes=img_bytes, model = model, curr_image = session['img'])
            regen_image = True
            if pred != session['label'] and pred != 'no':
                response = "this {} looks like a {}. must not be from our gallery!".format(session['label'], pred)
                session['level'] += 1
            else:
                response = "our art!! stop, thief!"
                session['yolo'] += 1

            if session['yolo'] > 3:
                session['yolo'] = 0
                session['level'] = 0
                response = "you have to move to escape the consequences of your art crimes. try again!"

    if session['level'] >= MIN_LEVEL:
        response = FLAG
    elif response is None:
        response = "you've managed to steal %d paintings. maybe one more will be enough!" % session['level']

    if regen_image or not MUST_REPEAT_CAPTCHA:
        img, label = gen_img()
        session['img'] = img
        session['label'] = label
    else:
        img = session['img']

    return render_template('index.html', response = response, b64png = img)

@app.errorhandler(RuntimeError)
def error_handler(e):
    return "haha lol something broke"

if __name__ == '__main__':
    app.run(host='0.0.0.0', port=1337)

We have a web service that prompts players with a blurry “challenge” image and lets us upload our own “player” images. The task is to submit 50 “player” images that appear similar to the “challenge” image according to imagehash.average_hash(), but gives a different prediction when passed through a machine learning image classifier that is hidden from the player (therefore it is a “black box”).

We can write some helper functions to interact with the server. We can test that it works by submitting back the challenge image; it should fail the machine learning classifier check.

python

import requests
import re
import base64

from PIL import Image
import io
import imagehash

s = requests.Session()

# url = "https://blackbox-web.chal.uiuc.tf/"
url = "http://localhost:1337/"

def query():
    res = s.get(url)
    challenge_b64 = re.search(r'src="data:image/png;base64,(.*)"/>', res.text).group(1)
    challenge_bytes = base64.b64decode(challenge_b64)
    challenge_im = Image.open(io.BytesIO(challenge_bytes))
    prompt = re.search(r'id="response">(.*)</div', res.text).group(1)
    return challenge_im, prompt

def answer(player_im):
    player_im.save("tmp.png")
    res = s.post(url, files={
        "file": open("tmp.png", "rb")
    })
    prompt = re.search(r'id="response">(.*)</div', res.text).group(1)
    return prompt

challenge_im, prompt = query()
print(prompt)

print("Submitting challenge image...")
ans_prompt = answer(challenge_im)
print(ans_prompt)

output

you&#39;ve managed to steal 0 paintings. maybe one more will be enough!
Submitting challenge image...
our art!! stop, thief!

Broken challenge solution

python

print("Broken challenge solution")
url = "https://blackbox-web.chal.uiuc.tf/"
while True:
    print("o", end="", flush=True)
    challenge_im, prompt = query()
    # just submit the challenge image lol
    ans_prompt = answer(challenge_im)
    if "uiuctf" in ans_prompt:
        print()
        print(ans_prompt)
        break

output

Broken challenge solution
oooooooooooooooooooooooooooooooooooooooooooooooooo
uiuctf{oh_n0_my_b4nksy}

To solve this challenge, it turns out that imagehash.average_hash() is weak. We can check its source code on github:

python

def average_hash(image, hash_size=8, mean=numpy.mean):
  # docstring...
  if hash_size < 2:
    raise ValueError("Hash size must be greater than or equal to 2")

  # reduce size and complexity, then covert to grayscale
  image = image.convert("L").resize((hash_size, hash_size), Image.ANTIALIAS)

  # find average pixel value; 'pixels' is an array of the pixel values,
  # ranging from 0 (black) to 255 (white)
  pixels = numpy.asarray(image)
  avg = mean(pixels)

  # create string of bits
  diff = pixels > avg
  # make a hash
  return ImageHash(diff)

The hash does the following:

Convert the input image to a 8x8 grayscale image
Calculate the average brightness of all pixels
For each pixel, return 1 if brighter or 0 if darker than the average and return this as the “hash”
The “difference” between two images is the hamming distance between each image’s “hash” (i.e. the number of 1s/0s that are different)

To generate an image that looks very different (to us and to the machine learning image classifier) from some original image but has the same image hash, we can try to directly generate an image from the image hash. We can parse the image hash as a 8x8 1-bit black/white image, then resize and convert it to the required dimensions and color channels using nearest neighbour scaling.

This image is guaranteed to produce the same imagehash.average_hash(), but since it looks like black and white noise the image classifier would likely give a random prediction which is enough to pass the server’s check.

python

import numpy as np

def generate_player_image(challenge_im):
    challenge_hash = imagehash.average_hash(challenge_im)
    player_im = Image.fromarray(np.asarray(challenge_hash.hash * 255, np.uint8), "L")
    player_im = player_im.resize((224, 224), Image.NEAREST)
    player_im = player_im.convert("RGB")
    player_hash = imagehash.average_hash(player_im)
    assert challenge_hash - player_hash == 0
    return player_im

challenge_im, prompt = query()
print(prompt)
player_im = generate_player_image(challenge_im)

print("Submitting image...")
ans_prompt = answer(player_im)
print(ans_prompt)

output

you&#39;ve managed to steal 0 paintings. maybe one more will be enough!
Submitting image...
this ship looks like a truck. must not be from our gallery!

We can run this in a loop to get the flag. Progress is reset once we fail 4 checks. If the classified output is indeed random, there is a 90% chance that the check passes, which adds up to a 20% chance of us reaching 50 “stolen images” without getting reset.²

python

s = requests.Session()

images = []

while True:
    challenge_im, prompt = query()
    player_im = generate_player_image(challenge_im)
    ans_prompt = answer(player_im)
    if "stop, thief!" in ans_prompt:
        print("x", end="", flush=True)
    elif "try again!" in ans_prompt:
        print("X")
        print("retry")
        images = []
    else:
        print("o", end="", flush=True)
    images.append(challenge_im)
    images.append(player_im)
    if "uiuctf" in ans_prompt:
        break
print()
print(ans_prompt)

output

xxoooooxoX
retry
oxooooooooooxooxooooooooooooX
retry
ooooxxooooooooooooxooooX
retry
[... several more lines ...]
ooooxoooooxoooooooxooooX
retry
ooooooooooooooooooooxooooooooooxooooooooooooooooxoooo
uiuctf{fake_flag}

Collage visualisationpython
def concat_h(im1, im2):
    dst = Image.new('RGB', (im1.width + im2.width, max(im1.height, im2.height)))
    dst.paste(im1, (0, 0))
    dst.paste(im2, (im1.width, 0))
    return dst

def concat_v(im1, im2):
    dst = Image.new('RGB', (max(im1.width, im2.width), im1.height + im2.height))
    dst.paste(im1, (0, 0))
    dst.paste(im2, (0, im1.height))
    return dst

collage = None
for i in range(0, len(images), 10):
    images_row = images[i:i+10]
    collage_row = None
    for image in images_row:
        if collage_row is None:
            collage_row = image
        else:
            collage_row = concat_h(collage_row, image)
    if collage is None:
        collage = collage_row
    else:
        collage = concat_v(collage, collage_row)
collage.resize((1000, 1000)).save("collage.png")

Well even though the stolen pictures look pretty bad at least we have the flag.

Other Challenges

mom can we have AES

First blood 🩸 at 7:33:08 from CTF start.

We are given two services running scripts that does a AES cipher negotiation handshake with each other.

After understanding the handshake protocol, MITM the handshake between the kid and mom services while forcing both of them to use AES-ECB (including an extra plaintext "finish" which for some reason the mom service does not send). This turns the kid service into a AES-ECB encryption oracle that returns encrypt(user_input + flag) and is vulnerable to chosen plaintext attack.

Exploit code

python

from pwn import *
import string

# Open connection to both services
conn_mom = remote("mom-can-we-have-aes.chal.uiuc.tf", 1337)
conn_kid = remote("mom-can-we-have-aes.chal.uiuc.tf", 1338)

# pow
conn_mom.recvline()
conn_kid.recvline()

# cipher
ciphers = conn_kid.recvline().strip()
assert ciphers == b"AES.MODE_CBC, AES.MODE_CTR, AES.MODE_OFB, AES.MODE_EAX, AES.MODE_ECB"
conn_mom.sendline(b"AES.MODE_ECB") # MITM

# client random
client_random = conn_kid.recvline().strip()
conn_mom.sendline(client_random)

# server cert
server_sig = conn_mom.recvline().strip()
conn_kid.sendline(server_sig)

# selected cipher
selected_cipher = conn_mom.recvline().strip()
assert selected_cipher == b"AES.MODE_ECB"
conn_kid.sendline(selected_cipher)

# server random
server_random = conn_mom.recvline().strip()
conn_kid.sendline(server_random)

# premaster key
premaster = conn_kid.recvline().strip()
conn_mom.sendline(premaster)

# confirm cipher
confirm_cipher = conn_kid.recvline().strip()
conn_mom.sendline(confirm_cipher)

# enc("finish")
finish_signal = conn_kid.recvline().strip()
conn_mom.sendline(finish_signal)
conn_kid.sendline(b"finish")

# done
# conn_mom.clean(0.5), conn_kid.clean(0.5)
conn_mom.close()

# now its AES-ECB with chosen plaintext attack

def query_ecb(x):
    conn_kid.sendline(x.hex().encode())
    res = bytes.fromhex(conn_kid.recvline().strip().decode())
    return res

pad_char = b"\x00"
known = pad_char * 16

def chunked(x, bs=16):
    return [
        x[i:i+16]
        for i in range(0, len(x), 16)
    ]

charset = string.ascii_letters + string.digits + string.punctuation
while known[-1:] != b"}":
    print(".", end="", flush=True)
    probes = b"".join([
        (known + s.encode())[-16:]
        for s in string.ascii_letters + string.digits + string.punctuation
    ])
    pos = len(known) - 16
    pad_amount = 64 - 1 - pos

    res = query_ecb(probes + pad_char * pad_amount)
    chunked_res = chunked(res)
    leak = chunked_res.index(chunked_res[-3])
    known += charset[leak].encode()
print()
print(known[16:])

output

[x] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1337
[x] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1337: Trying 35.184.164.169
[+] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1337: Done
[x] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1338
[x] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1338: Trying 35.184.164.169
[+] Opening connection to mom-can-we-have-aes.chal.uiuc.tf on port 1338: Done
[*] Closed connection to mom-can-we-have-aes.chal.uiuc.tf port 1337
...........................
b'uiuctf{AES_@_h0m3_b3_l1ke3}'

That-crete Log

Server generates some random token $t$ and gives the player 5 queries. For each query, the player gives a large prime $N_i < 2^{1024}$ where $(N_i-1)$ must have at least one large factor $> 2^{512}$ . The servers returns some $x_i$ and $\text{out}_i$ where $\text{out}_i = x_i^{\text{flag} \oplus t} \mod N_i$ .

For each query, we generate some weak $N_i$ where $N_i-1$ has many small prime factors $p_0, p_1 \ldots$ and a single large prime factor $P$ . We can solve the discrete log of $\text{out}_i^{P}$ with base $x_i^{P}$ in $\mathbb{Z_{N_i}}$ . Taking the variables to power $P$ constrains the values to a smooth subgroup of order $\Pi p_i$ , which can be solved quickly using a Pohlig-Hellman attack.

We use sagemath discrete_log to calculate the discrete logs of each query and then combine the results of the five queries with the Chinese Remainder Theorem.

Exploit code

sage

from pwn import *

def prime_bits(b):
    return random_prime(2^b, 2^(b-1))

def generate_n(large_prime_bits, small_primes_bits, twiddle_bits):
    while True:
        # Large P
        P = prime_bits(large_prime_bits)
        # Many small p
        ps = [prime_bits(i) for i in small_primes_bits]
        Pps = prod([2] + ps + [P])
        for _ in range(100):
            # Try multiple final p to get a prime
            twiddle_p = prime_bits(twiddle_bits)
            try_n = (Pps * twiddle_p + 1)
            if try_n.is_prime():
                return try_n, P, [2] + ps + [twiddle_p, P]

r = remote("log.chal.uiuc.tf", 1337)
r.recvuntil(b"Here's your token for the session: ")
token = int(r.recvline().strip().decode())
print(f"{token=}")
print()

crt_as = []
crt_bs = []

for i in range(5):
    n, P, phi_fac = generate_n(520, [24] * 10, 24)

    phif_str = " ".join([str(i) for i in phi_fac])
    r.sendlineafter(b"Give me the prime factors of phi(N): ", phif_str.encode())

    r.recvuntil(b"x = ")
    x = int(r.recvline().strip().decode())
    r.recvuntil(b"out = ")
    out = int(r.recvline().strip().decode())

    # solve dlog
    F = Zmod(n)
    dlog = discrete_log(F(out) ^ P, F(x) ^ P)
    sub_ord = (F(x) ^ P).multiplicative_order()
    crt_as.append(dlog)
    crt_bs.append(sub_ord)

    print(f"{n=}")
    print(f"{x=}")
    print(f"{out=}")
    print(f"{dlog=}")
    print(f"{sub_ord=}")
    print()

# recover flag
flag_xor_token = crt(crt_as, crt_bs)
print(f"{flag_xor_token=}")
flag = flag_xor_token ^^ token
print(f"{flag=}")
print(bytes.fromhex(hex(int(flag))[2:]))

output

[x] Opening connection to log.chal.uiuc.tf on port 1337
[x] Opening connection to log.chal.uiuc.tf on port 1337: Trying 34.173.46.25
[+] Opening connection to log.chal.uiuc.tf on port 1337: Done
token=115252043315080069211788772230314084802563899042985991925257357186927446363299309635373613108414589115358266051022252187528388847666857527405160229592646186108033797035085098953200798381099445461872492552834838652566156561617685989075600098851555872052050167773044480799160522843214337051725369058341493731639

n=69635454756751799481415582317476981430621765708074021414358874214845092138094564588686841247519856695969980422111599843270550289916617064173830320861856120197817671039070441497371288159352474016518038351800044447189223419759012813159
x=28302940667249362207703596076255021827770991980563165469733062507004668230889325321072871703941254994716136779722484966080094540108061769069849002976378828851638078671654386026709383862687349223879193789664864617754700299232177573035
out=48107037550886295321718456586517872045047310909276626755118749952460521232376518208249156658168527791626462643846120513150280059933761402734065112503337439667931875279748215099324865636675619768210833122110307522819080316766251348169
dlog=8612051295706839306831523889958944733992081503658072067380812951193173638460
sub_ord=25813918870933342269418063125043767802478258726550619630209528056341236784042

n=45828029433747157675399881769005283518516193497533845156529996240159608192193485862407313997709318053681859748245663132978468137845352937385250515311688842834490319778406740535227383425971558330501723726434281432302905813024459443
x=25646286238606298340161560239154851115147485651837340332627583669429629740496676312974156458858668232289136385430008036397146503967500902346894845051821940392784850095962580427838176068895967528609227725385125025595976772139250912
out=22529718033215420820287757229074227472667246159384175617736111924741652381524131244640543351537345606594148124291624968320882548074859904597126503017212314503339754413503352695885202418972771699966226777540493718049118776505245133
dlog=1496648107171608713805115036809364718263399320834451980923625857412828623
sub_ord=7179416748041412429954008939713230796726916019767891520748090139219511763

n=1023752912938122410991964620427236136282070106815285413887834390415216181047962716537638532301284514528522158632149248113368760709817967591029590768259254524721540829588119419877365099436989223421581704835827373092109911652295768287
x=15490026862734541013199745371862814899564204758034030996344814324820315770080613253133293656729097316907299484206720271214175488917138286641561515133516507315175869469169237174147420334020426158544481837803788053784022491686949833
out=650395057196598545700352250088991602592086591085660354600772913640749886512238503427407306749748299271734135433597158788633165878413277959610699073572163955103373640471244039174079413046416249966154306207138109695979295410130977390
dlog=204679363701310119362029977086463635363182886547493699697741322029033483122
sub_ord=331811046131816017120137974316285406800515048800797656390573370205871750278

n=62205794681819896299758744506255713424509051024295191282665723066317892084372605806891702494811419438401591823027538485994229241817023720776308040173492052972662983042575035588177986681166836147619612040027367167809051476596516619
x=14276117861308164001524425277999951844486905754775258414261803770068575377248154916721308976546421596445087254397519355085069999505335788371011657470764554227793932637416518527170011361100353841945993540838162874145411248947877872
out=45121563106322833847624946083758775393966742894641994399515539172001340591959104571008430658323373399351435710920509465892432283724037287412021526506626845303035769405573840794793747378914467417747884278777700636922431539140980921
dlog=23832521455608546729542248798936120079841565911378336871027973382331234160
sub_ord=25274565380179279578068779314602568324201090111549349508558395752353870971

n=920725946338160142404273122024039708047775811997680754212777306370505555931102385741857139522976137425655711530946337010560216162821271521706044660384774154785090308486621866900599359122243469163232463123725942871835827040272243
x=31113876882981691716417421442307101560974379575525982700886886865075024306685248605187337368290817926652444193278451130058243184271094407686054444597587822770837190171825102147148552644935303072517727213265217304904769483656479
out=517069572339441381177765471578371066995581795965045443828698658989746251833644908553893161482194811347058620378088799134557163614684017777360027413381518556863178975895651512385067754797664769213895801635403527131622792843285305
dlog=265945125210347853690884126510209242660211527277564361222015103925045386
sub_ord=352011957599792857045722514424931866478894442759028506792402521275423986

flag_xor_token=115252043315080069211788772230314084802563899042985991925257357186927446363299309635373613106073445508447780869746654561204091042819896442188622774804714584659925780244729607561956298282654292986976744165731664953095975706803338597485639769903958704751347552825835314241071286691484426565959837161880006607178
flag=2529701069150202415145759245888660935698948454718014822883116354342940915912102610953531198507000362037519603585304850716182610938231315800778127873706339271012829908434694336380279513706795940071841884610930876231805
b'uiuctf{w0w_1_th0ughT_Th4t_discr3te_L0g_w4s_h4rD_f04_s4f3_prim2s!1!_d91ea3cf4a3daaf0604520}'

Elliptic Clock Crypto

We are given logs of a diffie hellman key exchange using a circle curve and an encrypted secret.

Points on the ellipse curve have additive order $p-1$ which is smooth, therefore we can solve the discrete log with the Pohlig-Hellman attack. After monkeypatching __mul__, __neg__, __sub__, __hash__, parent()(0) and is_zero() of ClockPoint, we can use sagemath discrete_log with the various points given in the handout. After solving for Alice’s secret key, complete the key exchange and decrypt the flag.

Also see a similar challenge The True ECC from SEETF 2022.

Exploit code

sage

from hashlib import md5
from Crypto.Cipher import AES

p = 62471552838526783778491264313097878073079117790686615043492079411583156507853
Fp = Zmod(p)

# copied from ecc.py
def scalar_mult(x, n):
    y = ClockPoint(0, 1)
    if n == 0: return y
    if n == 1: return x
    while n > 1:
        if n % 2 == 0:
            x = x + x
            n = n // 2
        else:
            y = x + y
            x = x + x
            n = (n-1) // 2
    return x + y

class ClockPoint:
    # copied from ecc.py
    def __init__(self,x,y):
        x, y = Fp(x), Fp(y) # new
        assert int(x*x + y*y) == 1
        self.x = x
        self.y = y
    def __str__(self):
        return f"({self.x},{self.y})"
    def __eq__(self, other):
        return str(self) == str(other)
    __repr__ = __str__
    def get_hash(self):
        return md5(str(self).encode()).digest()
    def __add__(self, other):
        x1,y1 = self.x, self.y
        x2,y2 = other.x, other.y
        return ClockPoint( x1*y2+y1*x2, y1*y2-x1*x2 )

    # monkeypatched
    def __mul__(self, other):
        return scalar_mult(self, other)
    def __neg__(self):
        return self * (p-2)
    def __sub__(self, other):
        return self + (-other)
    def parent(self):
        def inner(x):
            assert x == 0
            return ClockPoint(Fp(0),Fp(1))
        return inner
    def is_zero(self):
        return (self.x, self.y) == (0, 1)
    def __hash__(self):
        return hash((int(self.x), int(self.y)))

base_point = ClockPoint(
    34510208759284660042264570994647050969649037508662054358547659196695638877343,
    4603880836195915415499609181813839155074976164846557299963454168096659979337
)
alice_pk = ClockPoint(
    929134947869102207395031929764558470992898835457519444223855594752208888786,
    6062966687214232450679564356947266828438789510002221469043877962705671155351
)
bob_pk = ClockPoint(
    49232075403052702050387790782794967611571247026847692455242150234019745608330,
    46585435492967888378295263037933777203199027198295712697342810710712585850566
)

alice_sk = discrete_log(
    alice_pk, base_point, p-1,
    operation="+"
)
print(f"{alice_sk=}")

shared_key = (bob_pk * alice_sk).get_hash()
print(f"{shared_key=}")

enc = b' \xe9\x1aY.+E\xac\x1b\xc41\x1c\xf7\xba}\x80\x11\xa8;%]\x93\x88\x1fu\x87\x91\x88\x87\x88\x9b\x19'
flag = AES.new(shared_key.get_hash(), AES.MODE_ECB).decrypt(enc)
print(flag)

output

alice_sk=4639138469580745209791805177362345330837904161474827949276149771860091095988
shared_key=b'\xb5\xc3\xc99\xccR\xb1\x92\xa4,Gy\x05S\x1e\x88'
b'uiuctf{Circle5_ar3_n0t_ell1ptic}'

Footnotes

Specifically look for the 028201 hex sequence that should appear at the start of a >128 byte long integer chunk. There is one right after the 0x77 that was wrongly parsed as the tag, so we need to start parsing the chunk one byte later. ↩
Chance of $\geq 50/53$ trials succeeding with an individual probability of 90% is 21.053% using binomial probability. ↩