ImaginaryCTF 2022 Crypto Writeups
Changelog (last updated 2022-07-22)
Update 2022-07-22: Added Poker writeup, some touch-ups here and there.
Poker
By StealthyDev
In the early days of online poker rooms, the game would get cracked and players would play with perfect knowledge of the upcoming hands… Can you deal out the next two games correctly?
Attachments: poker.py cards.22.07.16.txt
8 solves, 495 points
Challenge poker.py
from random import getrandbits from math import prod HEARTS = "🂱🂲🂳🂴🂵🂶🂷🂸🂹🂺🂻🂽🂾" SPADES = "🂡🂢🂣🂤🂥🂦🂧🂨🂩🂪🂫🂭🂮" DIAMONDS = "🃁🃂🃃🃄🃅🃆🃇🃈🃉🃊🃋🃍🃎" CLUBS = "🃑🃒🃓🃔🃕🃖🃗🃘🃙🃚🃛🃝🃞" DECK = SPADES+HEARTS+DIAMONDS+CLUBS # Bridge Ordering of a Deck ALPHABET52 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnop_rstuvw{y}" CARDS_PER_DEAL = 25 assert CARDS_PER_DEAL % 2 == 1 MAX_DEAL = prod(x for x in range(len(DECK) - CARDS_PER_DEAL + 1, len(DECK) + 1)) DEAL_BITS = MAX_DEAL.bit_length() def text_from_cards(string): return string.translate(string.maketrans(DECK, ALPHABET52)) def deal_game(): shuffle = getrandbits(DEAL_BITS) % MAX_DEAL deck = list(DECK) deal = "" while shuffle > 0: deal += deck.pop(shuffle % len(deck)) shuffle //= len(deck) + 1 while len(deal) < CARDS_PER_DEAL: deal += deck.pop(0) return deal def print_puzzle(): with open("cards.txt", "w") as cards_file: for i in range(750): table = deal_game() cards_file.write(f"Game {i+1}:\n") for i in range((CARDS_PER_DEAL - 5) // 2): cards_file.write(f"{i + 1}: {table[i * 2]}{table[i * 2 + 1]} ") cards_file.write("\nTable: {}{}{} {} {}\n\n".format(*table[CARDS_PER_DEAL - 5:]))
We get a poker simulator which deals cards based on the python random() PRNG and are told to predict two deals after the end of the file.
By re-running some of poker.py locally, we find:
DEAL_BITS = 133 2 ** DEAL_BITS = 10889035741470030830827987437816582766592 MAX_DEAL = 7407396657496428903767538970656768000000
With some regex and careful implementation, we can convert the dealt cards back to a number x for each deal such that x = getrandbits(DEAL_BITS) % MAX_DEAL.
For each deal, one of two cases have occurred:
getrandbits(DEAL_BITS) < MAX_DEALandx = getrandbits(DEAL_BITS)getrandbits(DEAL_BITS) >= MAX_DEALandx = getrandbits(DEAL_BITS) - MAX_DEAL
We can split the first case depending on the value of x and rearrange to get three cases:
x < 2 ** DEAL_BITS - MAX_DEALandgetrandbits(DEAL_BITS) = xx >= 2 ** DEAL_BITS - MAX_DEALandgetrandbits(DEAL_BITS) = xx < 2 ** DEAL_BITS - MAX_DEALandgetrandbits(DEAL_BITS) = x + MAX_DEAL
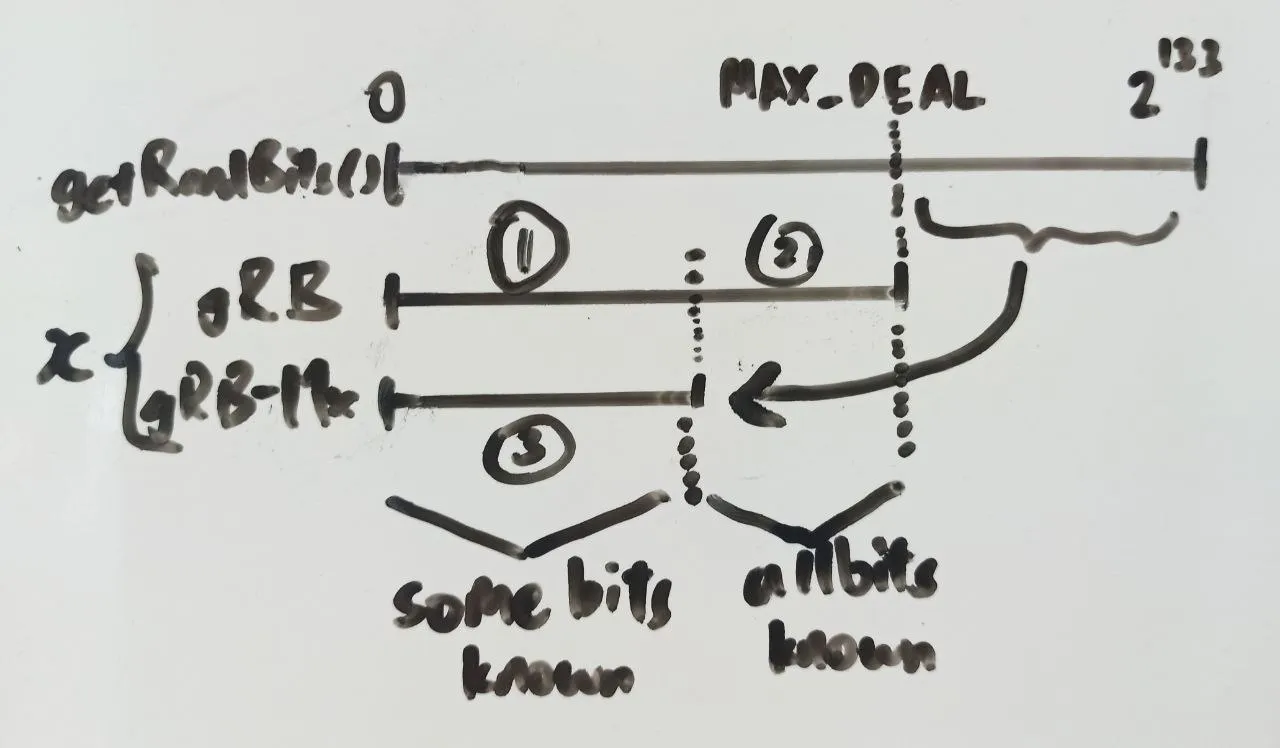
Note that from our perspective with only knowledge of , we are unable to differentiate between case 1 or 3. If our has a value that may have come from case 1 or 3, there are two possible values of getrandbits(DEAL_BITS). In case 2, this is only one possible value of getrandbits(DEAL_BITS). We can put this into a symbolic python PRNG cracker that supports unknown bits to recover the PRNG state. For case 1 and 3, we will only report bits which are the same in both x and x + MAX_DEAL, and any disagreeing bits will be labelled as unknown. In case 2, we know that getrandbits(DEAL_BITS) = x for sure and can report all bits of x to the PRNG solver.
To simplify implementation, only the low 128 bits were considered when recovering PRNG output and the upper 5 bits were discarded. Some quick estimations suggest that case 2 occurs around 36% of the time, giving an expected leak of 87 bits of PRNG state per deal. After testing, around 400 deal outputs are needed as input for the PRNG cracker to successfully recover the PRNG state, which can be confirmed by predicting the remaining 350 deals correctly. Finally, the flag is obtained by converting the 751st and 752nd deals to text.
Exploit code
from math import prod from random import seed, getrandbits import re # !wget \ # https://raw.githubusercontent.com/icemonster/symbolic_mersenne_cracker/main/main.py \ # -O untwister.py 2>/dev/null from untwister import Untwister HEARTS = "🂱🂲🂳🂴🂵🂶🂷🂸🂹🂺🂻🂽🂾" SPADES = "🂡🂢🂣🂤🂥🂦🂧🂨🂩🂪🂫🂭🂮" DIAMONDS = "🃁🃂🃃🃄🃅🃆🃇🃈🃉🃊🃋🃍🃎" CLUBS = "🃑🃒🃓🃔🃕🃖🃗🃘🃙🃚🃛🃝🃞" DECK = SPADES+HEARTS+DIAMONDS+CLUBS CARDS_PER_DEAL = 25 MAX_DEAL = prod( x for x in range(len(DECK) - CARDS_PER_DEAL + 1, len(DECK) + 1) ) DEAL_BITS = MAX_DEAL.bit_length() print("deal bits", DEAL_BITS) def deal_game_leak(frombits=None): if frombits is None: getrand = getrandbits(DEAL_BITS) else: getrand = frombits shuffle = getrand % MAX_DEAL shuffle_orig = shuffle deck = list(DECK) deal = "" deal_idxs = [] while shuffle > 0: deal_idx = shuffle % len(deck) deal_idxs.append(deal_idx) deal += deck.pop(deal_idx) shuffle //= len(deck) + 1 while len(deal) < CARDS_PER_DEAL: deal += deck.pop(0) return deal, getrand, shuffle_orig, deal_idxs def cards_to_deal_idxs(deal): deck = list(DECK) deal_idxs = [] for c in deal: deal_idx = deck.index(c) deck.pop(deal_idx) deal_idxs.append(deal_idx) return deal_idxs def deal_idxs_to_getrand(deal_idxs): cur_deck_len = len(DECK) - len(deal_idxs) + 1 acc = 0 for deal_idx in deal_idxs[::-1]: acc = acc * cur_deck_len + deal_idx cur_deck_len += 1 return acc def getrand_to_randbits(getrand): cap = DEAL_BITS // 32 * 32 bits = bin(getrand + 2 ** cap)[-cap:] return bits def getrand_to_randbits_mod(getrand): if (getrand + MAX_DEAL) >= 2 ** DEAL_BITS: return getrand_to_randbits(getrand) a = getrand_to_randbits(getrand) b = getrand_to_randbits(getrand + MAX_DEAL) res = "".join([ i if i == j else "?" for i, j in zip(a, b) ]) return res # Sanity checks test_seed = 0 seed(test_seed) for _ in range(10): deal = deal_game_leak() deal_idxs = cards_to_deal_idxs(deal[0]) assert(deal_idxs == deal[3]) getrand = deal_idxs_to_getrand(deal_idxs) randbits = getrand_to_randbits_mod(getrand) assert(all([ i == j for i, j in zip(randbits, bin(deal[1])[-128:]) if i != "?" ])) def pipeline(cards): known = getrand_to_randbits_mod( deal_idxs_to_getrand( cards_to_deal_idxs( cards ) ) ) return [ known[i:i+32] for i in range(0, 128, 32) ][::-1] + ["?" * 32] with open("poker/cards.22.07.16.txt", "r") as f: raw = f.read() deals = raw.strip().split("\n\n") print("num deals", len(deals)) def parse_deal(deal, check_num): deal_num = re.search( r"Game (\d+):", deal, re.UNICODE | re.MULTILINE ).group(1) deal_num = int(deal_num) assert check_num == deal_num cards = re.sub( r"[ -~\n]*", "", deal, re.UNICODE | re.MULTILINE ) assert(len(cards) == CARDS_PER_DEAL) return cards all_deals = [ parse_deal(deal, deal_idx + 1) for deal_idx, deal in enumerate(deals) ] print() print("deals") for i in all_deals[:5]: print(i) all_deals_pred = [ i for deal in all_deals for i in pipeline(deal) ] print() print("pipeline output") for i in all_deals_pred[:5]: print(i) use = 400 print() print("submitting") ut = Untwister() for i in all_deals_pred[:use * 5]: ut.submit(i) print("solving") rng = ut.get_random() print("verify") for i in all_deals[use:]: test = deal_game_leak(rng.getrandbits(DEAL_BITS))[0] assert(test == i) print("flag") ALPHABET52 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnop_rstuvw{y}" def text_from_cards(string): return string.translate(string.maketrans(DECK, ALPHABET52)) for i in range(3): deal = deal_game_leak(rng.getrandbits(DEAL_BITS))[0] print(text_from_cards(deal), end="") print()
deal bits 133 num deals 750 deals 🂦🃄🂭🃚🃎🂽🂡🃙🃖🂾🃉🃅🃊🂲🂧🃈🃝🃃🃂🃓🂳🂱🂸🃕🂪 🃒🃉🂡🃄🃕🂣🃓🃈🃃🂥🃍🂧🃔🃆🃚🂱🂨🂮🃙🂢🂳🂫🃗🂩🂴 🂺🂱🃘🃈🃋🂳🂨🃕🃑🂪🂢🃍🂲🂴🃁🃆🃛🂥🂮🂹🂻🂵🃖🂧🂩 🃔🃓🂢🃚🃖🂵🃉🂽🃍🃅🂲🃞🂮🂷🃇🂺🂪🃘🂳🂦🂸🃆🃄🂤🂴 🂢🃍🃕🃅🂻🃗🂸🃇🃙🂹🃔🃃🂱🃉🂥🂫🂧🂵🃎🂭🃊🂩🂷🃝🃓 pipeline output 0??11?00010101101101110001001101 1?111??1?????0000??01?0?100?01?? 0010????1100???0????00???011??0? 0?010???1????1????0???010111???? ???????????????????????????????? submitting STT> Solving... solving STT> Solved! (in 8.13s) verify flag ictf{CheaTINg_PsuEdoRAnDOm_BITgenEratioN}bcdfhjklpGJTYgCOrVswXhAj{aQnSPckfW
Secure Encoding: Base64
By puzzler7
Base64 is my favorite encryption scheme.
Attachments: encode.py out.txt
10 solves, 492 points
Challenge encode.py
from base64 import b64encode from random import shuffle charset = b'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/=' shuffled = [i for i in charset] shuffle(shuffled) d = {charset[i]:v for(i,v)in enumerate(shuffled)} pt = open("flag.txt").read() while "\n\n\n" in pt: pt = pt.replace("\n\n\n", '\n\n') while ' ' in pt: pt = pt.replace(' ', ' ') assert all(ord(i)<128 for i in pt) ct = bytes(d[i] for i in b64encode(pt.encode())) f = open('out.txt', 'wb') f.write(ct)
Most fun challenge of the CTF IMO.
We get a file encode.py and a very large base64 encoded text out.txt. By reading encode.py we understand that it does the following:
- Reads text from a file
- Trims every instance of 3 or more newlines to 2 newlines
- Trims every instance of 2 or more spaces to 1 space
- Asserts that all text has
ord(c) < 128 - Encodes text as base64
- Substitutes each base64 character to another unique base64 character
Our task is to recover the original text despite the base64 character set being substituted.
The first observation is to ensure valid base64 padding. We see the = padding character in the middle of the text which is invalid base64, and also that the 2 character only appears at the end of out.txt. We can make a naive swap of = with 2 to make the padding valid.
We need to solve for some permutation / mapping of 64 encrypted characters to 64 original characters. The next observation to make is that the more correct assignments of shuffled charset to original charset we have, the more the base64 decoded text will “look” like a valid input text. This suggests a simulated annealing approach to recover the shuffle permutation.
First we make a mutation function which swaps 2 (or rarely 3 or 4) characters with each other inside the ciphertext, allowing us to iterate through permutation search space.
We then make a fitness function which grades decryptions on how “valid” it is:
- We assign a heavy penalty to decryptions containing patterns that definitely cannot appear in the plaintext, such as
- Illegal characters
ord(c) >= 128 - Illegal substrings such as three newlines
"\n\n\n"and two spaces" "(but I skipped these in the final exploit)
- Illegal characters
- Assuming the text is printable ASCII, we assign a small penalty to non-printable characters that have
ord(c) < 128 - Assuming the text is english, we add a bonus to decryptions containing text patterns which frequently appear in english such as
- Whitespace (
" ","\n") - Alphabets
- Common english bigrams (
"th","he") and trigrams ("the","and") - Valid english punctuation (
", ",". ") - And several other patterns. See here for the stats used.
- Whitespace (
Next we create a temperature evaluation function to probabilistically accept or reject new permutations based on a “temperature” parameter and the improvement of fitness from last iteration. We should accept any permutations that improve the fitness, but at the same time we want to give permutations with poorer fitness a small chance to be accepted to avoid being stuck in local minima.
Finally we create a scheduler function which keeps track of overall best permutations and decryption so far while adjusting temperature over time, also known as a cooling schedule.
To keep runtime fast, we trim the ciphertext to the first 40 thousand base64 characters (i.e. first 30 thousand bytes of plaintext).
After around 5 minutes of compute over 4 threads, most of the text is readable and we can find most of the flag as well!
Exploit code
from collections import Counter from base64 import b64decode from random import choice, sample, random, seed from string import printable, ascii_letters from numpy import linspace from tqdm.auto import tqdm from multiprocessing import Pool with open("b64/out.txt", "r") as f: raw = f.read() # 2 is the original padding character print("Least common", Counter(raw).most_common()[-3:]) print("Tail", raw[-5:]) # swap 2 and = raw = raw.replace("2", "@").replace("=", "2").replace("@", "=") print("Total length", len(raw)) # https://www3.nd.edu/~busiforc/handouts/cryptography/cryptography%20hints.html non_printable_charset = set(range(128)) - set(printable.encode()) whitespace_charset = set(" \n".encode()) alphabet_charset = set(ascii_letters.encode()) one_score = { i: 0 for i in range(256) } for i in range(128, 256): one_score[i] = -1000 for i in non_printable_charset: one_score[i] = -10 for i in whitespace_charset: one_score[i] = 4 for i in alphabet_charset: one_score[i] = 2 two_patterns_more = [ ". ", ", ", ".\n", "\n" # whoops the last "\n" should have been "\n\n" ] two_patterns = [ "th", "er", "on", "an", "re", "he", "in", "ed", "nd", "ha", "at", "en", "es", "of", "or", "nt", "ea", "ti", "to", "it", "st", "io", "le", "is", "ou", "ar", "as", "de", "rt", "ve", ] two_patterns_less = [ " T", " O", " A", " W", " B", " C", " D", " S", "E ", "S ", "T ", "D ", "N ", "R ", "Y ", "F ", ] two_score = {} for i in two_patterns_more: two_score[i.encode()] = 10 for i in two_patterns: two_score[i.encode()] = 5 for i in two_patterns_less: two_score[i.encode()] = 1 three_patterns = [ "the", "and", "tha", "ent", "ion", "tio", "for", "nde", "has", "nce", "edt", "tis", "oft", "sth", "men", " a ", " i ", ] three_score = { i.encode(): 10 for i in three_patterns } four_patterns = [ " of ", " to ", " in ", " it ", " is ", " be ", " as ", " at ", " so ", " we ", " he ", " by ", " or ", " on ", " do ", " if ", " me ", " my ", " up ", " an ", " go ", " no ", " us ", " am ", ] four_score = { i.encode(): 10 for i in four_patterns } def swap(x, *swaps): assert(len(swaps) >= 2) sub = {i: j for i, j in zip(swaps, swaps[1:] + swaps[:1])} return "".join([sub.get(i, i) for i in x]) b64_charset = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/' def mutate(x): while True: swap_len = choice([2, 2, 2, 2, 3, 4]) swaps = sample(b64_charset, swap_len) x = swap(x, *swaps) if choice([True, True, True, False]): return x def fitness(x): x = b64decode(x) n = len(x) acc = 0 for i in range(n): c = x[i] cc = x[i:i+2] ccc = x[i:i+3] cccc = x[i:i+4] acc += ( one_score[c] + two_score.get(cc, 0) + three_score.get(ccc, 0) + four_score.get(cccc, 0) ) return acc / n def mutate_and_fitness(x): x = mutate(x) return x, fitness(x) def check_temp(fit_delta, temp): if fit_delta > 0: return True return - temp * random() < fit_delta take = 40000 print("Using first b64 characters", take) cur = raw[:take] cur_fit = fitness(cur) best = cur best_fit = cur_fit # Nothing up my sleeve, https://remywiki.com/1116 seed(1116) schedule = sum([ list(linspace(1, 0.0001, 200)) * 30, list(linspace(0.5, 0.0001, 200)) * 10, list(linspace(0.1, 0.0001, 200)) * 10, ], []) since_new_best = 0 stall_limit = 5 pbar = tqdm(schedule) with Pool(processes=4) as pool: for temp in pbar: muts = pool.map(mutate_and_fitness, [cur] * 4) mut, mut_fit = max(muts, key=lambda x: x[1]) pbar.set_description( f"Best: {best_fit:.03f} " f"Temp: {temp:.02f} " f"Cur: {cur_fit:.03f} " f"Stall: {since_new_best} " f"Mut: {mut_fit:.03f} " ) if mut_fit > best_fit: best, best_fit = mut, mut_fit since_new_best = 0 continue since_new_best += 1 if since_new_best == stall_limit: since_new_best = 0 cur, cur_fit = best, best_fit continue if check_temp(mut_fit - cur_fit, temp): cur, cur_fit = mut, mut_fit pln = b64decode(best) print("First 1000 characters") print("=" * 80) print(pln[:1000].decode()) print("=" * 80) print("Found ictf", b"ictf" in pln) if b"ictf" in pln: flag_pos = pln.index(b"ictf") print(pln[flag_pos-10:flag_pos+50])
Least common [('F', 57), ('T', 46), ('2', 2)] Tail hoP22 Total length 597924 Using first b64 characters 40000 0%| | 0/10000 [00:00<?, ?it/s] First 1000 characters ================================================================================ The Project Gutenberg eBooj of The Picture of Dorian Gray, by Nscar Wilde This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Prozect Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBooj. Title+ The Picture of Dorian Gray Author+ Oscar Wilde Release Date+ October, 19=4 [eBooj #174] [Most recently updated+ February 3, 2022] Language: English Produced by+ Judith Boss. HTML version by Al Haines. **: START OF THE PROJECT GUTEOBERG EBONK THE PICTURE NF DORIAN GRAY :** The Picture of Dorian Gray by Nscar Wilde Contents THE PREFACE CHAPTER I. CHAPTER II. CHAPTER III. CHAPTER IV. CHAPTER V. CHAPTER VI. CHAPTER VII. CHAPTER VIII. CHAPTER IX. CHAPTER ================================================================================ Found ictf True b'useless.\n\nictf~all_encodings_are_nothing_but_art}\n\nOSCAR WIL'
Living Without Expectations
By Robin_Jadoul
Sometimes you just gotta have some fun implementing bare hardness assumptions.
Attachments: lwe.py output.txt
10 solves, 492 points
lwe.py has rand() that provides a deterministic stream of integers from 0 to 7. The script generates a 69-dimension vector with elements 0 or 1. For each bit of the flag, we are given:
- 69x69 matrix with random elements
- 69-dimension vector equal to if the flag bit is 0; or
- 69-dimension vector with random elements if the flag bit is 1
This looks like learning with errors, where is the secret key.
Assuming that the flag begins with ictf{, the first bit of i should be 0 and we should get the case. We can solve for using Babai’s closest vector algorithm. Notably, both the noise as well as the secret key is small in comparison to the magnitude of and the elements in and . The closest lattice point is therefore likely to reveal . After this, we can check for each flag bit using and inspecting if recovered vector is a possible error from by looking at its magnitude.
Exploit code
import numpy as np # https://jgeralnik.github.io/writeups/2021/08/12/Lattices/ def babai_closest_vector(B, target): # Babai's Nearest Plane algorithm M = B.LLL() G = M.gram_schmidt()[0] small = target for _ in range(1): for i in reversed(range(M.nrows())): c = ((small * G[i]) / (G[i] * G[i])).round() small -= M[i] * c return target - small q = 2**142 + 217 n = 69 nseeds = 142 with open("lwe/output.txt", "r") as f: raw = f.read() lines = raw.strip().split("\n") print("data size", len(raw), len(lines)) def parse_arr(arr): arr = arr.strip(" ][").split(", ") return np.array([ int(i.strip("'")[2:], 16) for i in arr ]) def parse_line(line): a, _, b = line.strip(" []").partition("] [") return parse_arr(a), parse_arr(b) # take first bit, should be 0 which = 0 a, b = parse_line(lines[which]) a = a.reshape((n, n)) # use only first 10 elements of b samples = 10 lock = 1 lockval = 2 ** 200 mat = [ [0 for x in range(n + samples + lock)] for y in range(n + samples + lock) ] for i in range(n): mat[i][i] = 1 for j in range(samples): mat[i][n+j] = a[j][i] for i in range(samples): mat[n+i][n+i] = q for i in range(samples): mat[n+samples][n+i] = -b[i] mat[n+samples][n+samples] = lockval vec = [0] * n + [0] * samples + [lockval] mat = Matrix(mat) vec = vector(vec) cv = babai_closest_vector(mat, vec) s = list(cv)[0:n] s = np.array(s) print("s", s) res = "" for which in range(len(lines)): a, b = parse_line(lines[which]) a = a.reshape((n, n)) if -7 * n < ((a @ s % q) - b).sum() <= 0: res += "0" else: res += "1" print("flag bin", res[:50], "...") pln = bytes.fromhex(hex(int(res, 2))[2:]) print(pln)
data size 67729514 336 s [1 1 1 0 0 0 0 0 0 0 1 1 1 0 1 0 0 1 0 1 1 0 1 1 0 0 0 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 1 1 1 1 0 1] flag bin 01101001011000110111010001100110011110110110110000 ... b'ictf{l4tt1c3_crypt0_t4k1ng_0v3r_th3_w0rld}'
Lorge
By Robin_Jadoul
I guess smoll needed a revenge after all 😭
Attachments: lorge.py output.txt
29 solves, 433 points
From lorge.py, we see that and are smooth. We first try to factor using Pollard p-1 attack and generator , but at some point goes from a coprime number to straight away. This is because some largest prime factor of and are the same. Since the initial run stopped at the largest prime factor , we can instead start with generator and re-try the attack which succeeds.
Exploit code
from tqdm.auto import tqdm from gmpy2 import mpz, next_prime, log, floor, powmod, gcd with open("lorge/output.txt", "r") as f: raw = f.read() n, e, ct = [int(i.partition(" = ")[2]) for i in raw.strip().split("\n")] n = mpz(n) cap = mpz(2 ** 25) def pollard_rho_step(g, q): r = mpz(floor(log(cap) / log(q))) z = q ** r return powmod(g, z, n) leak = [] while True: g = mpz(2) cur = mpz(2) for i in leak: g = pollard_rho_step(g, i) pbar = tqdm(total=int(cap)) pbar.update(int(cur)) while cur < cap: g = pollard_rho_step(g, cur) check = gcd(g - 1, n) if check != 1: break nx = next_prime(cur) delta = nx - cur pbar.update(int(delta)) cur = nx if g == 1: print("leak common prime factor", cur) leak.append(cur) else: break p = gcd(g-1, n) q = n // p assert(p * q == n) phi = (p-1) * (q-1) d = powmod(e, -1, phi) pln = powmod(ct, d, n) bytes.fromhex(hex(int(pln))[2:])
0%| | 0/33554432 [00:00<?, ?it/s] leak common prime factor 19071329 0%| | 0/33554432 [00:00<?, ?it/s] b'ictf{why_d1d_sm0ll_3v3n_sh0w_up_on_f4ct0rdb???_That_m4d3_m3_sad!}'
stream
By Eth007
HELP! I encrypted my files with this program I downloaded from the internet. Can you recover my 42-byte flag?
37 solves, 390 points
Open stream binary with ghidra and grok.
Decompile of stream binary

The binary encrypts text with this procedure:
- Read an input file specified in
argv[1] - Process 8 bytes of input at a time as a 64 bit unsigned integer
- Xor the input integer with a 64 bit unsigned integer key specified in
argv[2] - Square the key
- Repeat until all of the input file is processed
- Write the output to a file specified in
argv[3]
What happens to input files that need padding to the nearest 8 bytes? We can run the script locally with a dummy key to test.
$ python -c "print('\x00' * 42, end='')" > zeros.txt $ ./stream zeros.txt 7 zeros.enc.txt $ hexdump -C -v zeros.txt 00000000 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................| 00000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................| 00000020 00 00 00 00 00 00 00 00 00 00 |..........| 0000002a $ hexdump -C -v zeros.enc.txt 00000000 07 00 00 00 00 00 00 00 31 00 00 00 00 00 00 00 |........1.......| 00000010 61 09 00 00 00 00 00 00 c1 f6 57 00 00 00 00 00 |a.........W.....| 00000020 81 7d 05 a5 39 1e 00 00 01 3b 9b 6e 58 33 3c 30 |.}..9....;.nX3<0| 00000030 $ python -c "print(hex(pow(7, 2 ** 5, 2 ** 64)))" 0x303c33586e913b01
It seems like the trailing bits are padded with zeros before xor. Since the flag is 42 bytes there will be 6 zero bytes of padding. These tail 6 bytes of enc then leaks the high 6 bytes of key during the final iteration.
Assuming the flag starts with ictf{, we can use this to leak the low 5 bytes of key during the first iteration. The key * key operation is done on a unsigned long long, which acts like multiplication modulo 2**64. As a result of this nice modulo, the lower bits of key in later iterations only depends on the same lower bits of key in previous iterations. We can manually square key from first iteration to get the low 5 bytes of key in the final iteration. This way, we have leaked key.
We can recover key of earlier iteration using iterative square root modulo prime power of key from later iterations. The exploit uses z3 to calculate this square root. We can speed this up by early pruning if some key produces a non-printable flag.
Exploit code
import struct from z3 import * from tqdm.auto import tqdm from string import printable from itertools import product # for some reason sage is slow, so z3 to the rescue def sqrt_mod_2_64(x): x = int(x) res = [] a = BitVec("a", 64) while True: s = Solver() s.add(a * a == x) for soln in res: s.add(a != soln) if str(s.check()) == "unsat": break soln = s.model()[a].as_long() res.append(soln) return res with open("stream/out.txt", "rb") as f: enc_raw = f.read() enc_raw, len(enc_raw) enc = struct.unpack("<" + "Q" * 6, enc_raw) key_low_first = (struct.unpack("<Q", b"ictf{\x00\x00\x00")[0] ^ enc[0]) & 0xffffffffff key_low_final = pow(key_low_first, 2 ** 5, 2 ** 64) & 0xffffffffff print("final key low 5 bits".ljust(22), hex(key_low_final).rjust(18)) key_high_final = enc[5] & 0xffffffffffff0000 print("final key high 6 bits".ljust(22), hex(key_high_final)) key_final = key_low_final | key_high_final print("final key".ljust(22), hex(key_final)) charset = set(printable.encode()) def search(idx, key, data=""): pln_chunk = bytes.fromhex(hex((enc[idx] ^ key) + 2 ** 64)[3:]) if idx == 5: pln_chunk = pln_chunk[-2:] if not all([i in charset for i in pln_chunk]): return None data = pln_chunk[::-1].decode() + data print(idx, data.strip()) if idx == 0: return prev_keys = sqrt_mod_2_64(key) for prev_key in prev_keys: search(idx-1, prev_key, data) search(5, key_final)
final key low 5 bits 0x241d06d81 final key high 6 bits 0x2297b40241d00000 final key 0x2297b40241d06d81 5 } 4 901bf2e4} 3 ystream_901bf2e4} 2 ed_my_keystream_901bf2e4} 1 _rec0vered_my_keystream_901bf2e4} 0 ictf{y0u_rec0vered_my_keystream_901bf2e4}
hash
By Eth007
My passwords are safe and secure with the use of sha42!
nc hash.chal.imaginaryctf.org 133739 solves, 378 points
sha42 has poor confusion. Each byte of the hash output is effectively the xor of some subset of the initial input bytes, depending on the length of the input byte array. We can do a (dumb) symbolic run of the hash to identify which input bytes affect each output byte, then use these correlations with z3 to solve for a possible input which produces some hash.
Since the challenge service does not compare input lengths, we can fix a length of 30 and will always get (some) solution since we have 30 unknowns and 21 equations.
Exploit code
from collections import defaultdict from tqdm.auto import tqdm from z3 import * from pwn import * # original implementation config = [ [int(a) for a in n.strip()] for n in open("hash/jbox.txt").readlines() ] def sha42(s: bytes, rounds=42): out = [0]*21 for round in range(rounds): for c in range(len(s)): if config[((c//21)+round)%len(config)][c%21] == 1: out[(c+round)%21] ^= s[c] return bytes(out).hex() # generate confusion relations confusion = defaultdict(list) # confusion[hash_index] = [input_char_indexes] length = 30 for target in range(length): probe = [0 for _ in range(length)] probe[target] = 1 probe = bytes(probe) res = sha42(probe) res = bytes.fromhex(res) for idx, f in enumerate(res): if f == 1: confusion[idx].append(target) # unhash solver def unhash(chal): solver = Solver() cs = [ BitVec(f"c{i}", 8) for i in range(length) ] for sink in range(21): rhs = 0 for s in confusion[sink]: rhs = rhs ^ cs[s] solver.add(rhs == chal[sink]) solver.check() model = solver.model() res = bytes([ model[s].as_long() for s in cs ]) return res # sanity check chal = sha42(b"some_16char_pass") chal = bytes.fromhex(chal) assert sha42(unhash(chal)) == chal.hex() # run conn = remote("hash.chal.imaginaryctf.org", 1337) for _ in tqdm(range(50)): conn.recvuntil(b"sha42(password) = ") chal = conn.recvline() chal = bytes.fromhex(chal.strip().decode()) soln = unhash(chal) conn.sendline(soln.hex().encode()) print(conn.recvall())
[x] Opening connection to hash.chal.imaginaryctf.org on port 1337 [x] Opening connection to hash.chal.imaginaryctf.org on port 1337: Trying 34.90.15.213 [+] Opening connection to hash.chal.imaginaryctf.org on port 1337: Done 0%| | 0/50 [00:00<?, ?it/s] [x] Receiving all data [x] Receiving all data: 16B [x] Receiving all data: 95B [+] Receiving all data: Done (95B) [*] Closed connection to hash.chal.imaginaryctf.org port 1337 b'hex(password) = Correct!\nCongrats! Your flag is: ictf{pls_d0nt_r0ll_y0ur_0wn_hashes_109b14d1}\n\n'
otp
By Eth007
Encrypt your messages with our new OTP service. Your messages will never again be readable to anyone.
nc otp.chal.imaginaryctf.org 1337Attachments: otp.py
48 solves, 316 points
secureRand returns more 1 bits than 0 bits, specifically giving 1 bits around 70% of the time. Connect multiple times to get many flag ^ secureRand() and the true flag bits will be the less common bit at each position.
Exploit code
from pwn import * from tqdm.auto import tqdm from collections import Counter def char_to_bin(x): return bin(0x100 + x)[3:] # simulate secureRand bias jumbler = [] jumbler.extend([2**n for n in range(300)]) jumbler.extend([3**n for n in range(300)]) jumbler.extend([4**n for n in range(300)]) jumbler.extend([5**n for n in range(300)]) jumbler.extend([6**n for n in range(300)]) jumbler.extend([7**n for n in range(300)]) jumbler.extend([8**n for n in range(300)]) jumbler.extend([9**n for n in range(300)]) print( "Probability of 1", sum([1 if int(str(i)[0]) < 5 else 0 for i in jumbler]) / len(jumbler) ) conn = remote("otp.chal.imaginaryctf.org", 1337) # leak many xor-ed flag n_leaks = 100 data_raw = [] for _ in tqdm(range(n_leaks)): conn.sendline(b"FLAG") conn.recvuntil(b"Encrypted flag: ") res = conn.recvline() data_raw.append( bytes.fromhex(res.decode().strip()) ) # recover flag data = [ "".join([char_to_bin(j)for j in i]) for i in data_raw ] pln_bin = "".join([ "1" if Counter(i).most_common(1)[0][0] == "0" else "0" for i in zip(*data) ]) pln = bytes.fromhex(hex(int(pln_bin, 2))[2:]) print(pln)
Probability of 1 0.69875 [x] Opening connection to otp.chal.imaginaryctf.org on port 1337 [x] Opening connection to otp.chal.imaginaryctf.org on port 1337: Trying 35.204.97.207 [+] Opening connection to otp.chal.imaginaryctf.org on port 1337: Done 0%| | 0/100 [00:00<?, ?it/s] b'ictf{benfords_law_catching_tax_fraud_since_1938}\n'