Google CTF 2022 - OCR

Changelog (last updated 2022-07-11)

Update 2022-07-11: Done some reorganising, thanks to @daniellimws for the comments

Update 2022-07-09: It turns out I was overly cautious with the convex hull exploit. I’ve done some parameter tuning and the results are much better.

Train our neural network to read handwritten letters! I’m sure with the newest technological advances, you’ll be able to do it with a tiny network and just a handful of training images.

ocr.2022.ctfcompetition.com 1337

Attachment

Official challenge archive

208 points, 47 solves

Challenge server.pypython
# Copyright 2022 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

import numpy as np
import sys
import glob
import string
import tensorflow as tf
from keras.models import Sequential
from keras.layers.core import Dense, Flatten
from flag import flag
import signal

signal.alarm(120)

tf.compat.v1.disable_eager_execution()

image_data = []
for f in sorted(glob.glob("/images/*.png")):
    im = tf.keras.preprocessing.image.load_img(
        f, grayscale=False, color_mode="rgb", target_size=None, interpolation="nearest"
    )
    im = tf.keras.preprocessing.image.img_to_array(im)
    im = im.astype("float32") / 255
    image_data.append(im)

image_data = np.array(image_data, "float32")

# The network is pretty tiny, as it has to run on a potato.
model = Sequential()
model.add(Flatten(input_shape=(16,16,3)))
# I'm sure we can compress it all down to four numbers.
model.add(Dense(4, activation='relu'))
model.add(Dense(128, activation='softmax'))

print("Train this neural network so it can read text!")

wt = model.get_weights()
while True:
    print("Menu:")
    print("0. Clear weights")
    print("1. Set weight")
    print("2. Read flag")
    print("3. Quit")
    inp = int(input())
    if inp == 0:
        wt[0].fill(0)
        wt[1].fill(0)
        wt[2].fill(0)
        wt[3].fill(0)
        model.set_weights(wt)
    elif inp == 1:
        print("Type layer index, weight index(es), and weight value:")
        inp = input().split()
        value = float(inp[-1])
        idx = [int(c) for c in inp[:-1]]
        wt[idx[0]][tuple(idx[1:])] = value
        model.set_weights(wt)
    elif inp == 2:
        results = model.predict(image_data)
        s = ""
        for row in results:
            k = "?"
            for i, v in enumerate(row):
                if v > 0.5:
                    k = chr(i)
            s += k
        print("The neural network sees:", repr(s))
        if s == flag:
            print("And that is the correct flag!")
    else:
        break

tl;dr (spoilers!)

Craft model weights to turn ReLU layers into a comparison oracle to leak image brightness data and reconstruct image dataset locally. More efficient solutions exist involving step-wise activation of output layers and crafting convex hulls.

Recon

We are given a service that hosts a small neural network used to classify 16x16 RGB images into ASCII letters. The server lets us do the following:

Reset model weights to zero
Edit the model weights with a user-provided layer index, weight index and value
Run the model against multiple images, each containing one character of the flag. The service prints any ASCII character with prediction confidence $>0.5$ , otherwise it just prints '?'.

We can test some challenge code locally to learn about the model and understand the trainable parameters.

python

model = Sequential()

# Flattens the 16 x 16 x 3 input into a flat 768-wide vector
model.add(Flatten(input_shape=(16,16,3)))

model.add(
  # Passes through a dense layer to 4 outputs
  # i.e. "matrix multiplication with a (768 x 4) matrix
  # and adding a 4-wide bias vector"
  Dense(4,

  # Uses a rectified linear unit activation function on
  # this hidden layer
  # i.e. "anything less than 0 is set to 0"
  activation='relu'
))

model.add(
  # Passes through another dense layer to 128 outputs
  # i.e. "another matrix multiplication with a (4 x 128)
  # matrix and adding a 128-wide bias vector"
  Dense(128,

  # Uses the softmax activation function to find the
  # strongest prediction
  # i.e. "take the element-wise value of $e^{x_i}$ and
  # normalize the sum to 1"
  activation='softmax'
))

wt = model.get_weights()
weight_names = [
  "Dense (image => hidden)",
  "Hidden layer bias",
  "Dense (hidden => output)",
  "Softmax bias"
]
for i, n in zip(wt, weight_names):
    print(n, ":", i.shape)

output

Dense (image => hidden) : (768, 4)
Hidden layer bias : (4,)
Dense (hidden => output) : (4, 128)
Softmax bias : (128,)

Overall, we have 2 dense matrices and 2 bias vectors that we can manipulate.

Though the challenge description hints at actually training a model to properly classify text in the images, there’s many reasons why this is a bad idea:

We don’t have enough training data with colors / font / etc. similar to the flag images for training a general model
The architecture is very limited with only 4-wide hidden layer (even the simplest 2-layer MNIST models uses 300 hidden units)
A single ReLU layer is probably not enough non-linearity to model functions well

Since we have very granular control over model weights, we can instead try to leak the image data by focusing on single pixels and red/green/blue color channels at a time and finding some way to leak brightness of the image using the model predictions.

Leaking 1 bit per prediction using bias on ReLU

The first thing to do when interacting with the service is to zero out the model weights. If we ignore this, the initial model instance will contain random parameters and output garbage predictions.

To “focus” our model on only one pixel, we can update one weight between the pixel of interest $x$ and the first hidden layer node $h_0$ to $1$ . Changing which pixel is focused then requires two weight setting operations: one to reset the connection with the previous pixel and one update to connect the new pixel with $h_0$ .

We now want some way to craft the rest of the neural network parameters to test how activated the hidden node is; the prediction output should let us distinguish between a dark pixel and a bright pixel. One way to do this is to change the bias of $h_0$ . If we use a negative bias $-b$ on $h_0$ , a dark pixel $x<b$ will have $h_0 = 0$ after applying the ReLU function (anything less than $0$ is set to $0$ ), while a bright pixel $x>b$ will still have $h_0 > 0$ .

We can then use the second dense layer and connect $h_0$ to some output node with a very large positive weight. Suppose we choose node 49 corresponding to the character '1'. A dark pixel leads to the '1' output having zero activation, while a bright pixel leads to the '1' output being very positive.

With this strategy, a dark pixel will make all output nodes have the same activation of zero and the prediction script will default to the '?' label, while in the case of a bright pixel the activation of the '1' label will overwhelm the softmax and return a '1' label.

This way, we can differentiate between dark ( $x<b$ ) and bright ( $x>b$ ) pixels by setting up these model weights and checking if the output is '?' or '1'. This is effectively a comparison oracle.

Focused pixel:

Brightness:

0.36

Bias:

-0.50

If we pick a bias of $-0.5$ on $h_0$ , we can decide if pixels are darker or brighter than $0.5$ , which tells if the original 8-bit brightness is lesser or greater than $128$ ¹. Our strategy here therefore leaks 1 most significant bit of the image brightness data.

We can repeat this leak across all possible pixels and red/green/blue channels to reconstruct a 3-bit color depth version of the flag images. A sample exploit with some server interaction helper functions and the comparison leak is given below, which produces the following leaked image.

Exploit helper setuppython
from pwn import *
from tqdm.auto import tqdm
import numpy as np
from PIL import Image
from collections import Counter

context.log_level = "error"

# Avoid wasting time in .recvuntil
FAST = True
r = None

def solve_pow(chal):
    # wget https://goo.gle/kctf-pow -O pow.py
    from pow import solve_challenge
    return solve_challenge(chal)

def new_remote():
    # # local testing
    # r = process(["python3", "./server.py"])
    # return r

    r = remote("ocr.2022.ctfcompetition.com", 1337)
    r.recvuntil(b"kctf-pow) solve ")

    chal = r.recvline().decode().strip()
    soln = solve_pow(chal)
    r.sendline(soln.encode())
    return r

def menu():
    if not FAST:
        r.recvuntil(b"3. Quit\n")
    else:
        r.clean()
    return

def clear_weights():
    menu()
    r.sendline(b"0")

def set_weight(*data):
    menu()
    r.sendline(b"1")
    if not FAST:
        r.recvuntil(b"and weight value:\n")
    idx, val = [int(i) for i in data[:-1]], float(data[-1])
    req = " ".join([str(i) for i in idx] + [str(val)])
    r.sendline(req.encode())

def read_flag():
    menu()
    r.sendline(b"2")
    r.recvuntil(b"The neural network sees:")
    res = r.recvline().split(b"'")[1].decode()
    return res

def recover_image(leaked_data, brightness_map):
    flag_len = len(leaked_data[0])
    img = np.zeros([16, 16 * flag_len, 3], np.uint8)

    for k, v in leaked_data.items():
        cur = k
        channel, cur = cur % 3, cur // 3
        x, cur = cur % 16, cur // 16
        y = cur
        for idx, px in enumerate(v):
            dx = 16 * idx + x
            val = brightness_map[px]
            img[y][dx][channel] = val

    return Image.fromarray(img)

Comparison leakpython
# one bit comparison leak
output_base = ord("1")

def setup_leak():
    clear_weights()
    set_weight(1, 0, -0.5)
    set_weight(2, 0, output_base, 100)

last_focused_pixel = None
def focus_pixel(pixel_idx):
    global last_focused_pixel
    if last_focused_pixel is not None:
        set_weight(0, last_focused_pixel, 0, 0)
    set_weight(0, pixel_idx, 0, 1)
    last_focused_pixel = pixel_idx

leaked_data = {}
r = new_remote()
setup_leak()
for i in tqdm(range(16 * 16 * 3)):
    focus_pixel(i)
    leaked_data[i] = read_flag()
    if i < 5:
        print(leaked_data[i])

im = recover_image(leaked_data, {"?": 0, "1": 255})
im.save("comparison-leak.png")
im

output

?1?1?1?1???1??111????111?1??????1?
1?1?111111111?1???1?1???11???1111?
11?1?1111??1??1111?1?1?1??11???1?1
???1?1?1????1?1??????111?1?1???111
1?1?11?1?11?1?1??11?1???11?1?1?11?

Though the images aren’t very readable, some teams reported that this sufficient to get most of the flag and guess the rest. If any more image detail is required you can re-run the script with different bias values to get a more detailed image; the official solution repeats this using two different biases.

In terms of server interaction cost, this solution uses 4 weight setting operations for initial setup and 2 more per prediction to select a new pixel to leak. However, we can still do better!

Leaking 2 bits per prediction by cancelling out ReLUs

Since there are 4 hidden nodes in the neural network, we might as well use all of them by assigning different biases to each node.

\begin{align*} h_0(x) &= \max(x - 0.00, 0) \\ h_1(x) &= \max(x - 0.25, 0) \\ h_2(x) &= \max(x - 0.50, 0) \\ h_3(x) &= \max(x - 0.75, 0) \\ \end{align*}

We can craft the second dense layer parameters such that the output activation is some linear combination of $h_0-h_3$ before softmax. With the additional observation that we can use negative coefficients in the dense matrix, we can tune the model such that the outputs “take turns” to be positive.

To do this, add a positive weight between each hidden node $h_i$ and a respective output node $\text{out}_i$ , then a heavy negative weight between the next hidden node $h_{i+1}$ and $\text{out}_i$ . $\text{out}_i$ will be very activated while $h_i$ is active, but it will be deactivated right after $h_{i+1}$ is active, creating a step-wise function. An extra bias of $+5$ is added to avoid confusion with the other 124 output labels and to reach the $0.5$ reporting threshold.

\begin{align*} \text{out}_0(x) &= 5 + 100 \cdot h_0(x) - 1000 \cdot h_1(x) \\ \text{out}_1(x) &= 5 + 100 \cdot h_1(x) - 1000 \cdot h_2(x) \\ \text{out}_2(x) &= 5 + 100 \cdot h_2(x) - 1000 \cdot h_3(x) \\ \text{out}_3(x) &= 5 + 100 \cdot h_3(x) \end{align*}

Visualizationpython
import numpy as np
import matplotlib.pyplot as plt

inputs = np.arange(0, 256) / 255
inputs = inputs.astype(np.float32)

hidden_biases = [0.0, 0.25, 0.5, 0.75]
hidden = [
    np.clip(inputs - hidden_bias, 0, 1)
    for hidden_bias in hidden_biases
]

dense_weights = [
    [100, -1000, 0, 0],
    [0, 100, -1000, 0],
    [0, 0, 100, -1000],
    [0, 0, 0, 100]
]
dense_biases = [5, 5, 5, 5]

outputs = [
    np.clip((sum(i * j for i, j in zip(dense_weight, hidden)) + dense_bias), -2, 1000)
    for dense_weight, dense_bias in zip(dense_weights, dense_biases)
]

outputs_exp = np.exp(np.array(outputs))
outputs_exp_total = outputs_exp.sum(axis=0)
outputs_softmax = outputs_exp / outputs_exp_total

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(16, 5))

ax1.set_title("Final layer activation before softmax")
for i in outputs:
    ax1.plot(inputs, i)


ax2.set_title("After softmax")
ax2.set_xlabel("Input brightness")
for i in outputs_softmax:
    ax2.plot(inputs, i)

plt.legend(["out0", "out1", "out2", "out3"])

Focused pixel:

Brightness:

0.36

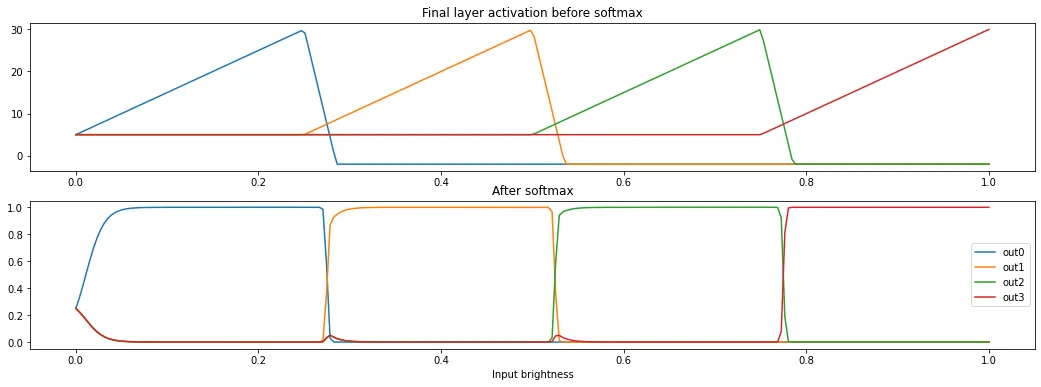
Each prediction will classify pixels into 4 different brightness values, leaking $\log_2(4)=2$ bits of data and letting us regenerate a 6-bit color depth version of the flag. With the same helper functions from earlier, we can write a new exploit to get the more detailed flag image:

Stepped ReLU leakpython
# two bit stepped leak
output_base = ord("1")

def setup_leak():
    clear_weights()
    set_weight(1, 0, 0)
    set_weight(1, 1, -0.25)
    set_weight(1, 2, -0.5)
    set_weight(1, 3, -0.75)
    set_weight(2, 0, output_base, 100)
    set_weight(2, 1, output_base, -1000)
    set_weight(2, 1, output_base + 1, 100)
    set_weight(2, 2, output_base + 1, -1000)
    set_weight(2, 2, output_base + 2, 100)
    set_weight(2, 3, output_base + 2, -1000)
    set_weight(2, 3, output_base + 3, 100)
    set_weight(3, output_base, 5)
    set_weight(3, output_base + 1, 5)
    set_weight(3, output_base + 2, 5)
    set_weight(3, output_base + 3, 5)

last_focused_pixel = None
def focus_pixel(pixel_idx):
    global last_focused_pixel
    for h in range(4):
        if last_focused_pixel is not None:
            set_weight(0, last_focused_pixel, h, 0)
        set_weight(0, pixel_idx, h, 1)
    last_focused_pixel = pixel_idx

leaked_data = {}
r = new_remote()
setup_leak()
for i in tqdm(range(16 * 16 * 3)):
    focus_pixel(i)
    leaked_data[i] = read_flag()
    if i < 5:
        print(leaked_data[i])

im = recover_image(leaked_data, {"?": 0, "1": 0, "2": 80, "3": 160, "4": 255})
im.save("stepped-leak.png")
im

output

23142423?1142234411123332332211?41
4242344433443131113142114321234341
4424233441131243432313142143231423
2214242321123132111123332313112444
32413414234?4132133131114323131342

19 weight setting operations are used for setup and another 8 operations per prediction are used to select a new pixel. This was the solution I used while the CTF was running and a full exploit can be found here.

Leaking more bits per prediction with convex hulls

Just to beat the dead horse, it turns out that this challenge can even be solved without using the ReLU to rectify the hidden layer and with just one hidden node! After setting up a hidden node that is equal to $x$ , we can craft multiple linear functions in the form $\text{out}_i(x) = m_i \cdot x + c_i$ using the second dense layer to form a convex hull. Each line segment of the hull will correspond to one output label. Depending on how bright the input pixel is, a different line segment of the convex hull will be highest, causing different predictions to be returned. We can therefore classify pixel brightness into as many brightness groups as we have line segments in the hull!

Here is a manual construction for a 7-segment convex hull below, which can leak 2.8² bits of image data per prediction. Using this strategy will require 15 setup operations and another 2 per prediction to pick a new pixel.

Visualizationpython
import numpy as np
import matplotlib.pyplot as plt

inputs = np.arange(0, 256) / 255
inputs = inputs.astype(np.float32)

output_weights = [-300, -100, -40, 0, 40, 100, 300]
output_biases = [60, 40, 26, 10, -13, -58, -240]

outputs = []
for output_weight, output_bias in zip(output_weights, output_biases):
    output = inputs * output_weight + output_bias
    output = np.clip(output, 0, 100)
    outputs.append(output)

outputs_exp = np.exp(np.array(outputs))
outputs_exp_total = outputs_exp.sum(axis=0)
outputs_softmax = outputs_exp / outputs_exp_total

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(16, 5))

ax1.set_title("Final layer activation before softmax")
for output in outputs:
    ax1.plot(inputs, output)

ax2.set_title("After softmax")
ax2.set_xlabel("Input brightness")
for output in outputs_softmax:
    ax2.plot(inputs, output)

ax1.legend(
  ["out0", "out1", "out2", "out3", "out4", "out5", "out6"],
  loc='upper center', ncol=7
)

Focused pixel:

Brightness:

0.36

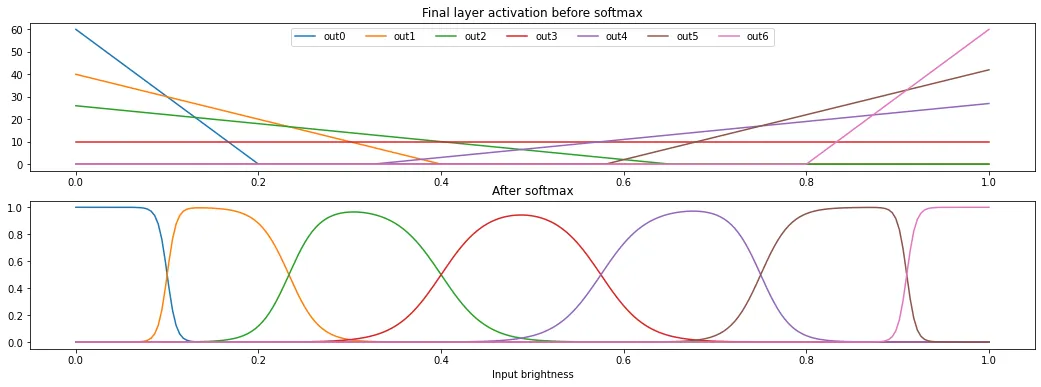
With more effort, convex hulls can be programmatically generated. A 16-segment piecewise linear approximation of $y = 720 \cdot (x-0.5)^2 + 5$ ³ can be used to leak 4 bits of image data per prediction⁴. This is a high enough precision that we even need to migrate from using ASCII digit labels to character labels. We can then generate these parameters and craft this final exploit to leak the most detailed flag image yet.

Constructing 16-segment convex hull parameters

python

import numpy as np
import matplotlib.pyplot as plt

splits = 16
n_inputs = 256

inputs = np.arange(0, n_inputs) / (n_inputs - 1)
inputs = inputs.astype(np.float64)
# yes, the model operates on float32 but tensorflow softmax is robust
# to floating point errors compared to manually running np.exp()

def approx_fn(x):
    x = 4 * (x - 0.5) ** 2
    x = x * 180 + 5
    return x
ylim = 200
hull = approx_fn(inputs)

ms = []
cs = []
for split in range(splits):
    x = (split + 0.5) / splits
    dx = 0.001
    y_minus_eps = approx_fn(x-dx)
    y = approx_fn(x)
    y_plus_eps = approx_fn(x+dx)
    m = (y_plus_eps - y_minus_eps) / (dx * 2)
    c0 = y - m * x

    ms.append(m)
    cs.append(c0)

fs = []
for m, c in zip(ms, cs):
    fs.append(inputs * m + c)
    mtext = f"{m:.02f}".rjust(7)
    ctext = f"{c:.02f}".rjust(7)
    print(f"{mtext} * x + {ctext}")

outputs = fs

outputs_exp = np.exp(np.array(outputs))
outputs_exp_total = outputs_exp.sum(axis=0)
outputs_softmax = outputs_exp / outputs_exp_total

fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(18, 9), sharex=True)

ax1.set_title("Approximating hull")
ax1.set_ylim(0, ylim)
ax1.plot(inputs, hull)

ax2.set_title("Final layer activation before softmax")
ax2.set_ylim(0, ylim)
for idx, output in enumerate(outputs):
    x = (idx + 0.5) / splits
    y = approx_fn(x) + ylim * 0.15

    ax2.plot(inputs, output)
    ax2.text(x, y, f"{ms[idx]:.2g}x + {cs[idx]:.2g}", ha="center")

ax3.set_title("After softmax")
ax3.set_xlabel("Input brightness")
ax3.set_ylim(0, 1)
ax3.axhline(0.5, color="grey", dashes=(3, 3))
for output in outputs_softmax:
    ax3.plot(inputs, output)

output

-675.00 * x +  184.30
-585.00 * x +  178.67
-495.00 * x +  167.42
-405.00 * x +  150.55
-315.00 * x +  128.05
-225.00 * x +   99.92
-135.00 * x +   66.17
 -45.00 * x +   26.80
  45.00 * x +  -18.20
 135.00 * x +  -68.83
 225.00 * x + -125.08
 315.00 * x + -186.95
 405.00 * x + -254.45
 495.00 * x + -327.58
 585.00 * x + -406.33
 675.00 * x + -490.70

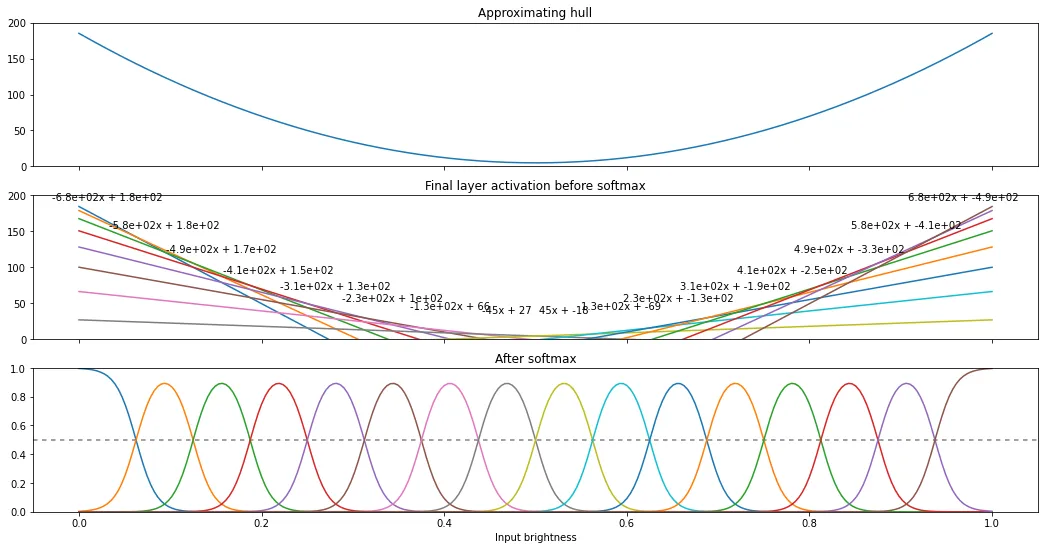
16-segment convex hull leakpython
# four bit convex hull leak
output_base = ord("A")

mcs = [
    (-750.0, 204.21875),
    (-650.0000000000057, 197.96875000000054),
    (-549.9999999999972, 185.46874999999955),
    (-449.99999999999574, 166.71874999999906),
    (-349.99999999999784, 141.71874999999937),
    (-250.0, 110.46875),
    (-150.00000000000034, 72.96875000000014),
    (-49.99999999999982, 29.21874999999992),
    (49.99999999999982, -20.781249999999904),
    (150.00000000000034, -77.0312500000002),
    (250.0, -139.53125),
    (349.99999999999784, -208.28124999999844),
    (449.99999999999574, -283.28124999999665),
    (549.9999999999972, -364.5312499999976),
    (650.0000000000057, -452.0312500000051),
    (750.0, -545.78125)
]

def setup_leak():
    clear_weights()
    set_weight(1, 0, 0)
    for idx, (m, c) in enumerate(mcs):
        set_weight(2, 0, output_base + idx, m)
        set_weight(3, output_base + idx, c)

last_focused_pixel = None
def focus_pixel(pixel_idx):
    global last_focused_pixel
    if last_focused_pixel is not None:
        set_weight(0, last_focused_pixel, 0, 0)
    set_weight(0, pixel_idx, 0, 1)
    last_focused_pixel = pixel_idx

leaked_data = {}

r = new_remote()
setup_leak()
for i in tqdm(range(16 * 16 * 3)):
    focus_pixel(i)
    leaked_data[i] = read_flag()
    if i < 5:
        print(leaked_data[i])

brightness_map = {
    chr(output_base + i): min(16 * i, 255)
    for i in range(16)
}
brightness_map["?"] = 0

im = recover_image(leaked_data, brightness_map)
im.save("convex-hull-leak.png")
im

output

FLAOGPHIACDMHGKOOCAAHLKJGLIG?ECAPA
PFOFJNOPMJMOKBLBEAKCN?BDPLGAGKMKPC
PM?OELKNNCEJCGNLOM?KALAOHCPJEIBNFL
FGAMGPHIGCDEJBKGDDAAEMLJGLCJBCGNPO
KHOAJNAPHJMAMCLFBJKCJABDPLHLDJAKPG

Using this strategy will require 33 setup operations and another 2 per prediction to pick a new pixel, giving us the largest amount of data leaked per operation so far. An executable jupyter notebook implementing the convex hull leak is available here.

Rounding everything up

To help our eyes out a bit, we can mask out the least common color in each 16x16 square of the flag.

Uncommon color maskingpython
def mask_flag_pixels(im):
    img = np.asarray(im)
    flag_len = img.shape[1] // 16
    for i in range(flag_len):
        ctr = Counter()
        for x in range(i * 16, (i + 1) * 16):
            for y in range(16):
                px = tuple(img[y, x])
                ctr[px] += 1
        flag_color = ctr.most_common(3)[-1][0]
        for x in range(i * 16, (i + 1) * 16):
            for y in range(16):
                px = tuple(img[y, x])
                if flag_color == px:
                    img[y, x, :] = [255, 255, 255]
                else:
                    img[y, x, :] = [0, 0, 0]

    return Image.fromarray(img, "RGB")

im_mask = mask_flag_pixels(im)
im_mask.save("masked-flag.png")
im_mask

We get the flag CTF{n0_l3aky_ReLU_y3t_5till_le4ky}.

More CTF challenges on toy neural networks

CTF SG 2021 Which Lee: defeating toy neural network with numerical instability

Archived challenge, writeup by myself and intended solution by author waituck
CTF SG 2022 Which Lee V2: defeating toy neural hash with adversarial generation

Writeup by Neobeo
SEETF 2022 Neutrality: solving an integer programming problem using machine learning

Archived challenge and writeup by JavaLim
Grey Cat The Flag 2022 Logical Computers: defeating toy neural hash with manual backpropagation

Archived challenge, writeup by aliencaocao

Footnotes

A bias of $-0.5$ effectively compares against $0.55$ / $140$ because of interference by the other 127 output nodes after softmax. The optimal bias can be found with some trial and error. ↩
$\log(7) \approx 2.8$ , but this assumes that the 7 segments are equally spaced (which it isn’t). ↩
In reality, modelling any function that has a strictly increasing first derivative will work. I found this function by starting out from a parabola with turning point at $(0.5, 0)$ and massaged the numbers from there. ↩
There is some data loss when two segments of the convex hull intersect leading to a prediction of '?'. You can remedy this by running the script a second time with a small $-\epsilon$ bias on the hidden layer and merging the results from both runs. ↩